引言
在日常使用百度和谷歌地图的时候,你有没有想过缩小后的整个世界的地图是什么样子的?
不过目前这两个地图的缩小比例都存在上限,无法在一个屏幕中全部展示。但你会发现东西向的地图是循环的,南北南的地图却是有限的,甚至看不到北极或者南极点。
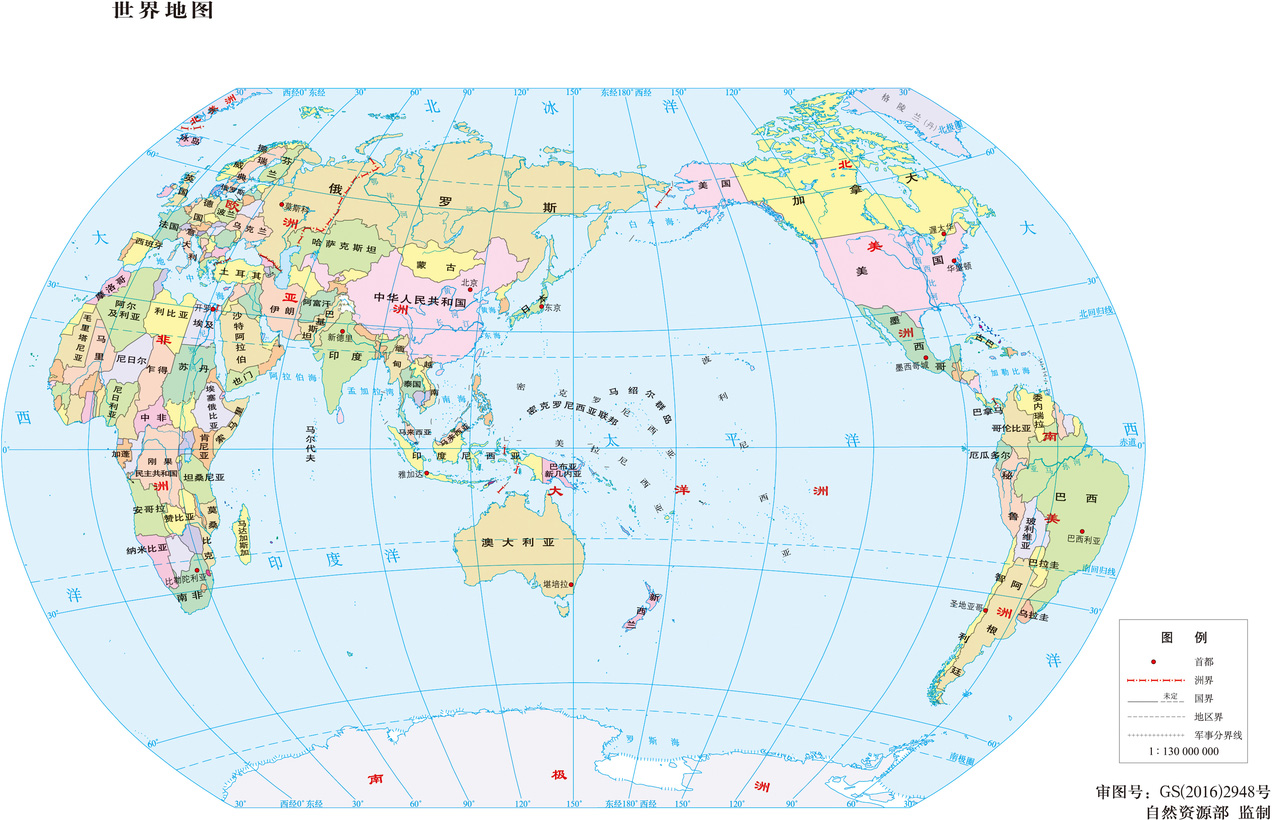
我通过一些小手段,我把完整的百度世界地图下载下来了,如下图:
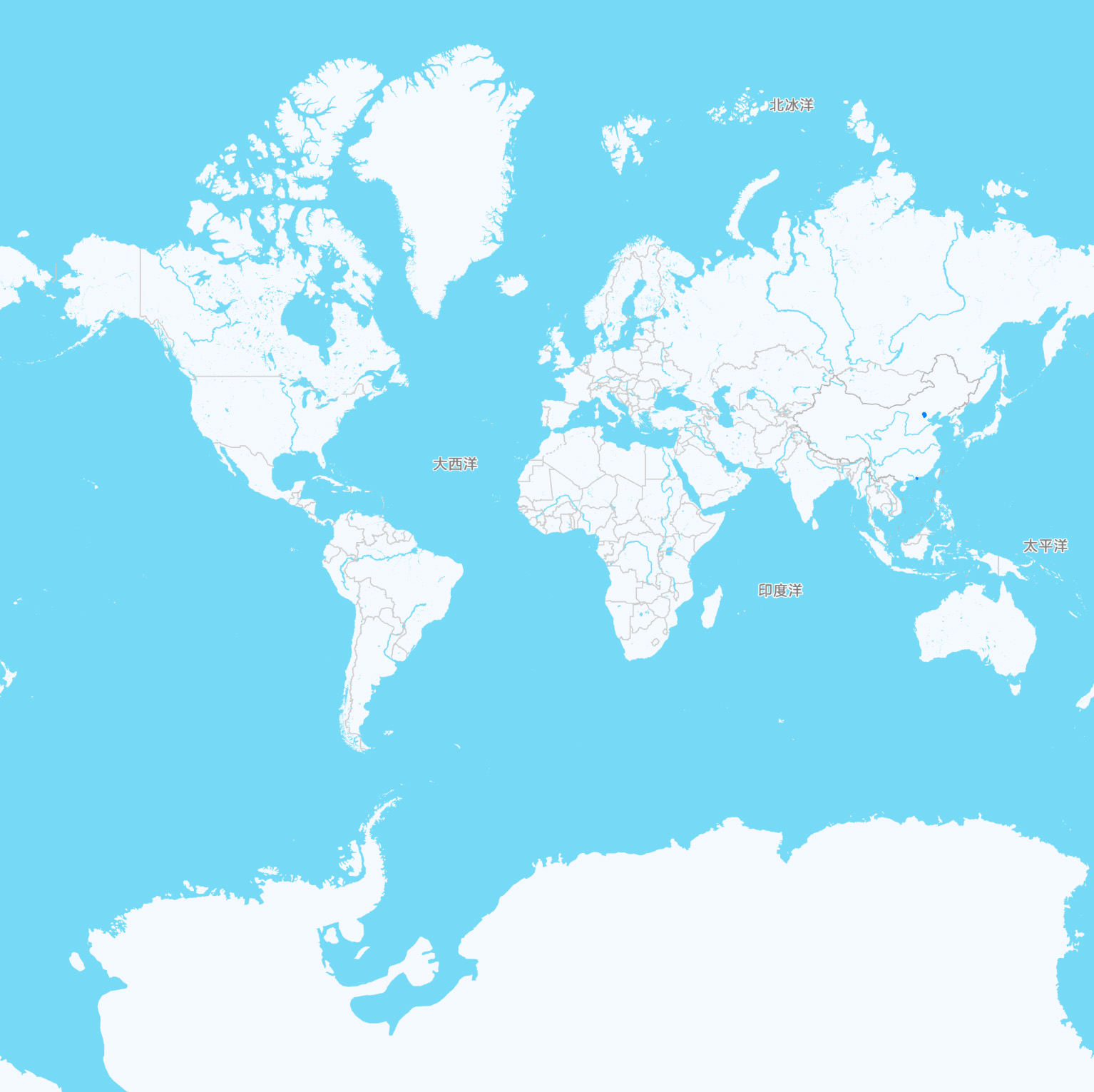
很快你会发现一些有趣的现象:
将东西循环的部分去掉,可以发现整张图类似于正方形;
南北极都被去掉了,最高的纬度也只有85° 左右;
靠近极点的部分,面积被放大的了,比如格林兰岛竟然比澳大利亚还大,实际格林兰岛面积216万平方公里,澳大利亚769万平方公里。
为什么是这样子的呢,或者说这张地图是遵循怎么样的标准画出来的呢?
要回答这个问题,我们需要先了解从经纬度的概念开始。
经纬线
在你生命的某个时间段里,以下的知识你一定了解,我们再来简单地复习一下,勾起那些已经死去的记忆。
经线
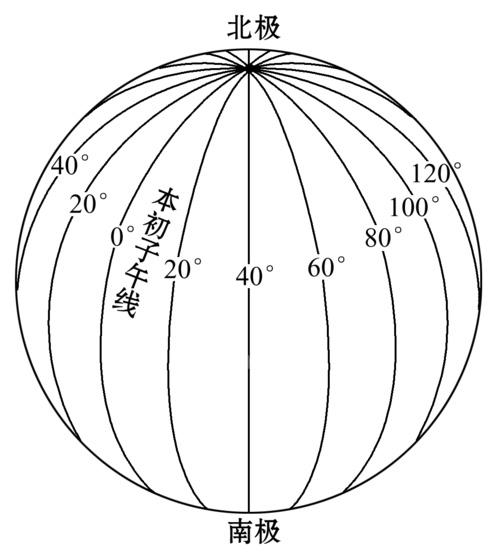
经线连接南北两极,每一条经线长度都相等,他的长度就是地球的周长,假设地球的半径为1,则周长为\(2π\)。
从本初子午线开始,往东180° 为东经,往西180° 为西经,西经一般以负数表示。
180° 与-180° 重合,这条线几乎与国际日界线重合(为了避免一些国家被日界线分割,国际日界线在一些地方有弯曲)。如上面的地图,从左到右就是-180° 到180° 。
纬线
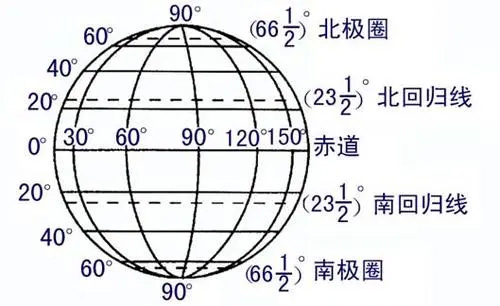
纬线是地球上的一点随自转所形成的圆,它与地轴垂直,与经线也垂直。
纬线最长的地方为0° ,也称之为赤道,往南北不断递增到90° ,北纬90° 为北极,南纬90° 为南极。
南纬一般用负数表示,例如南纬30° 也记作-30° 。
纬度是当前纬线上任意一点与球心的连线与赤道面所形成的夹角。
如下图是地球沿经线的横截面,计算A点的纬度,可以将A点与球心O做连线,他与赤道直径的夹角就是纬度。
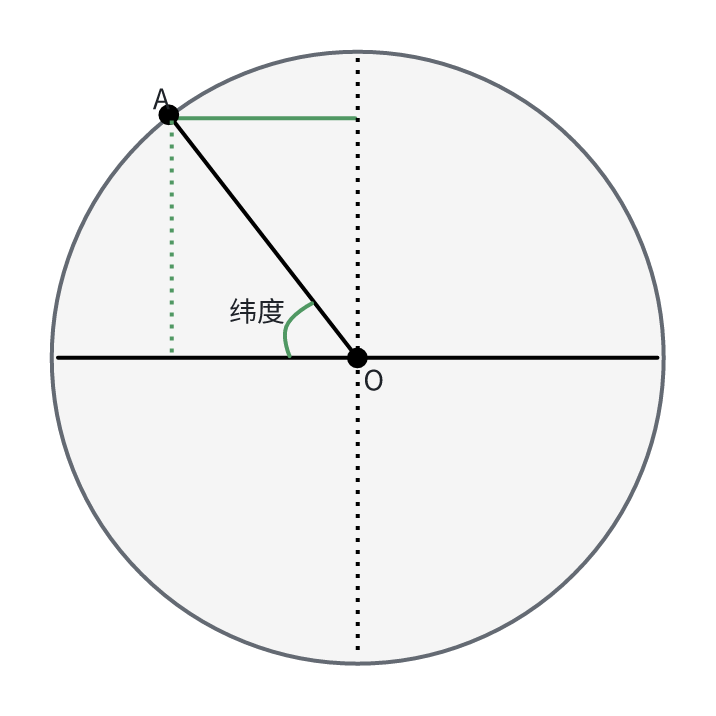
根据这一定义,假设地球的半径为1,A点的纬度是\(\theta\),将其转为弧度制的纬度\(\varphi=\frac{\theta}{180} \pi\),则A点所在纬线的长度为\(2\pi \cos\varphi\),\(\cos\varphi\)即为此点所在纬度圆的半径。
何为弧度制
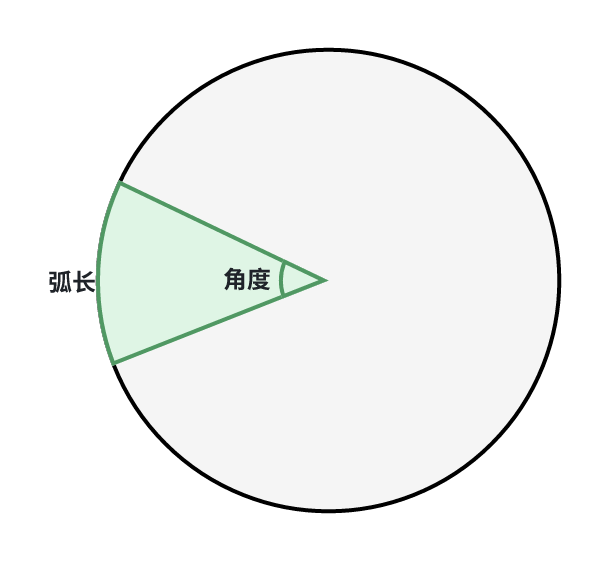
弧度制是用弧长与半径之比来度量角的大小的度量单位。
假设半径为\(r\)的圆中有一个角度为\(\theta\)的扇形(如下图),这个扇形在圆上的弧长为\(2\pi r\frac{\theta}{360}\),因为这段弧长占圆周长的\(\frac{\theta}{360}\)。
根据弧度的定义,此角在弧度制中的表示为\(\varphi = \frac{2\pi r\frac{\theta}{360}} {r} = \frac{\theta}{180}\pi\)。
墨卡托投影
有了以上的知识储备,我们回到刚开始的问题:谷歌和百度地图是如何绘制出来的?
投影方法和特点
首先为地球套上一个与赤道相切的圆柱体,再从球心出发,将地球表面投影到圆柱体内壁上,最后将圆柱体展开,即可得到我们想要的地图(如下图)。
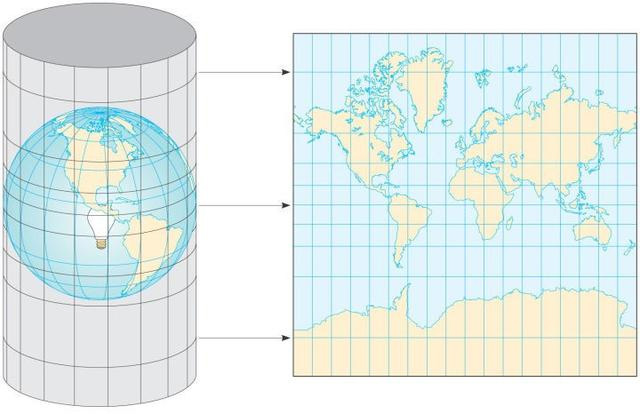
这种投影方法称为墨卡托投影,也称等角正轴圆柱投影。采用这种方法所投影出来的地图称为墨卡托地图。
之所以称为等角,是由于这种方法所投出来的大陆轮廓和形状与实际保持不变(即在任何一点往各个方向的比例尺保持不变)。另外他还能够显示任两点间的正确方位,所以他在海图、航路图中有广泛应用。
坐标转化
把墨卡托地图的赤道当成X轴,本初子午线当成Y轴,我们就得到一个直角坐标系。本节来计算经纬度与此坐标系之间的关系。
我们假设地球的半径为单位长度1,由于各个纬度上的纬线都被拉长成了赤道的长度,赤道的长度为\(2\pi\),各经线在赤道的分布又是均匀的,所以地图的横轴坐标的范围是\([-\pi,\pi]\)刚好与经度\([-180° ,180° ]\)的弧度制一一对应,假设经度为\(\lambda\),则\(x=\lambda\)。
而纬度并非均匀分布,越往高经度地区,纬线间隔越大。
在纬度\(\varphi\)处A点,此处的放大比例可以通过纬线的增加比例算出:地图上此处纬线的长度为赤道长度,即\(2\pi\),此处纬线的实际长度为\(2\pi \cos\varphi\)(根据纬度的定义),所以在A点处,长度放大的比例为\(\frac{1}{\cos\varphi}\)。
根据等角的定义,此处Y轴的放大比例应与此相等。增加微小的纬度\(d\varphi\),根据弧度制的定义,此时实际增加的长度为\(d\varphi\)(半径为1的圆,其弧度为角所在扇形的弧长),而地图上增加的长度为\(dy\),于是:
\(\frac{dy}{d\varphi} = \frac{1}{\cos\varphi}\),即\(dy= \frac{1}{\cos\varphi}d\varphi\),于是
\(y=\int_0^ydy = \int_0^\varphi \frac{1}{\cos\varphi}d\varphi\)
根据积分表查询得到公式\(\int\frac{dx}{\cos cx} = \frac{1}{c}\ln \vert \tan(\frac{cx}{2}+\frac{\pi}{4})\vert\),代入得:
\(y=\ln\vert tan(\frac{\pi}{4}+\frac{\varphi}{2}) \vert\)
反推求\(\varphi\)得:
\(\varphi = 2\arctan(e^y)-\frac{\pi}{2}\)
总结以上得到经线度与地图坐标的关系
\(\bbox[lightgreen,4px]{ \begin{cases} x=\lambda \\ \lambda = x \\ y=\ln|tan(\frac{\pi}{4}+\frac{\varphi}{2})| \\ \varphi = 2\arctan(e^y)-\frac{\pi}{2} \end{cases} }\)
从这个公式组中可以得出一些结论:
-
当纬度到达90° 也就是\(\frac{\pi}{2}\)时,\(y\)为无穷大(因为\(\tan\frac{\pi}{2}\)为无穷大,所以\(ln \vert \tan\frac{\pi}{2} \vert\)为无穷大)。事实上随着纬度增大,长度放大不断变大,到南北极为无穷大,这也就是为什么墨卡托地图越靠近两极,面积比实际要大得多;
-
在地图上,X轴的范围为\([-\pi,\pi]\),如果Y轴的范围也保持在这个范围,让地图呈现正方形,则Y轴能达到的纬度为\([-85° ,85° ]\)左右;可以令\(y=\pi\)或者\(y=-\pi\)来求出\(\varphi\)的值;
\(\varphi=(2arctan(e^\pi)-\frac{\pi}{2})\cdotp \frac{180}{\pi} = 85.0511287798066\)
Python代码实现:
(2*math.atan(math.pow(math.e,math.pi))-math.pi/2)*180/math.pi
其它的制图方式
除了墨卡托地图外,还有其它多种的制图方式,常见的如下图,他减少了两极的畸变,但并非等角。可以从这个网站上看到各式各样的制图方式。