狭义相对论假设/指导原则
1. 光速不变原理
真空中的光速在不同的惯性参考系中都是相同的。
即光速度不会随着光源的运动而发生改变,也不会随着参考系的变换而发生改变。
举例来说,假设一列以0.9\(c\)运动的列车在运动方向上发出一束光,此在不管在车内还是在车外所测得的光速都为光速\(c\)。
2. 相对性原理
在不同的惯性参考系中,一切物理规律都是相同的。
相对于牛顿提出的所有力学原理在所有惯性系中保持不变,狭义相对论将这一原理推广到了所有的物理理论,即所有物理理论在所有惯性系中都保持不变,你无法通过任何物理实验确定自己是在匀速直线运动还是静止。
狭义相对论的推论
1. 钟慢效应
结论:运动物体的时间流速\(t'\)相对于静止的物体流速\(t\)更慢,其关系为\(\bbox[lightgreen,4px]{t = {1 \over {\sqrt{1-({v \over c})^2}}}t'}\),其中\({1 \over {\sqrt{1-({v \over c})^2}}}\)为洛伦兹因子,一般记为\(γ\);速度越快,时间越慢。
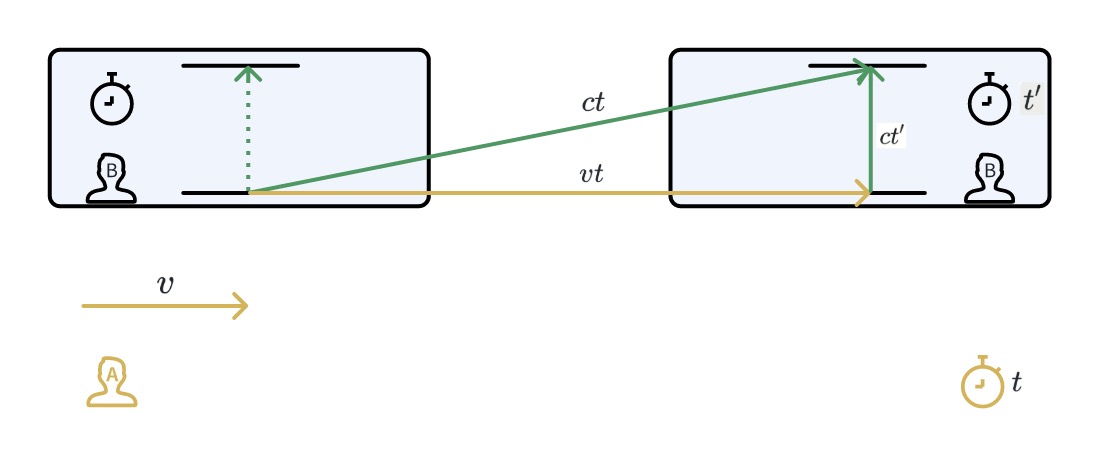
假设在一个惯性参考系统中,有一列匀速运动的火车,其速度为\(v\);
A静止地站在火车外,B位于火车内,相对火车静止;
此时火车内有一束光从地板发射到天花板;
对于火车内的B来说,光从地板到天花板所用的时间为\(t'\),走过的路径为\(ct'\);
对于火车外的A来说,光所运行的轨迹与B看到的不一样,假设A花了时间\(t\),由于光速在所有惯性系都为\(c\),所以在A看来,光所走的路程为\(ct\);
而火车此时运行的路程为\(vt\);
由勾股定理可知:\((vt)^2+(ct')^2=(ct)^2\),逐步求解\(t\):
\((c^2-v^2)t^2=c^2t'^2\)
\(t=\sqrt{\frac{c^2}{c^2-v^2}} t'={\frac{1}{\sqrt{1-({\frac{v}{c}})^2}}}t'\)
这里即可得出洛伦兹因子\(γ={1 \over {\sqrt{1-({v \over c})^2}}}\)。
由公式可知,当速度\(v\)远小于光速\(c\)时,\(γ\)几乎为0,也就是在低速状态下,\(t=t'\);
随着速度\(v\)增大逐渐接近光速时,\(γ\)也越来越大,即\(\frac{t}{t'}\)也越来越大,在A看来,B中的时间也越来越慢,这就是高速运动中的钟慢效应,速度越快,时间越慢。
钟慢效应也是相对的,将B与其所在的火车为参考系,则A在以速度\(v\)向后运动,在B看来,A的时间也会变慢。
2. 尺缩效应
结论:运动的物体,会在运动方向上发生长度收缩,收缩后的长度为\(\bbox[lightgreen,4px]{L' = L_0\sqrt{1-({v\over c})^2}}\),其中\(L_0\)为本征长度,即在相对静止的坐标系中测得的长度。
证明如下 :
假设从A点到B点的距离为\(L_0\),有一艘飞船以速度\(v\)从A驶向B;
对于飞船外的人看到这艘飞船所花的时间为\(t=\frac{L_0}{v}\);
而对于飞船内的人来说,由于钟慢效应,在他们看来,段路程所花的时间为\(t' = t\sqrt{1-({v\over c})^2}\);
所以他们所看到的A到B的距离为:\(L' = vt' = vt\sqrt{1-({v\over c})^2} = v {L_0 \over v}\sqrt{1-({v\over c})^2} = L_0\sqrt{1-({v\over c})^2}\)。
在上面的例子中,是以飞船为参考系,此时相对于飞船,外部的空间在不断后退,飞船内所看到空间的长度随着速度的增大不断缩小。
同理,在外部看来随着飞船速度增大,飞船在运动方向上的长度不断变小,这就是尺缩效应,即速度越快,长度越小。
3. 洛伦兹变换的推导
洛伦兹变换是两个惯性坐标系的转换,最早由洛伦兹为了解释迈克尔逊-莫雷实验中光速各向同速的实验结果而提出,后被爱因斯坦用于狭义相对论成为其基本方程组。
在钟慢效应中我们使用简单的方式推导出来洛伦兹因子,在本节中,我们从实际两个坐标系出发,来推导出洛伦兹变换的完整表达形式。
假设\(S\)和\(S'\)两个时空坐标系(包含三维空间\((X, Y, Z)\)和时间维度\(T\));在时间为0时,两个坐标系重合;
为了简化过程,坐标系\(S'\)以速度\(v\)沿\(X\)轴运动;
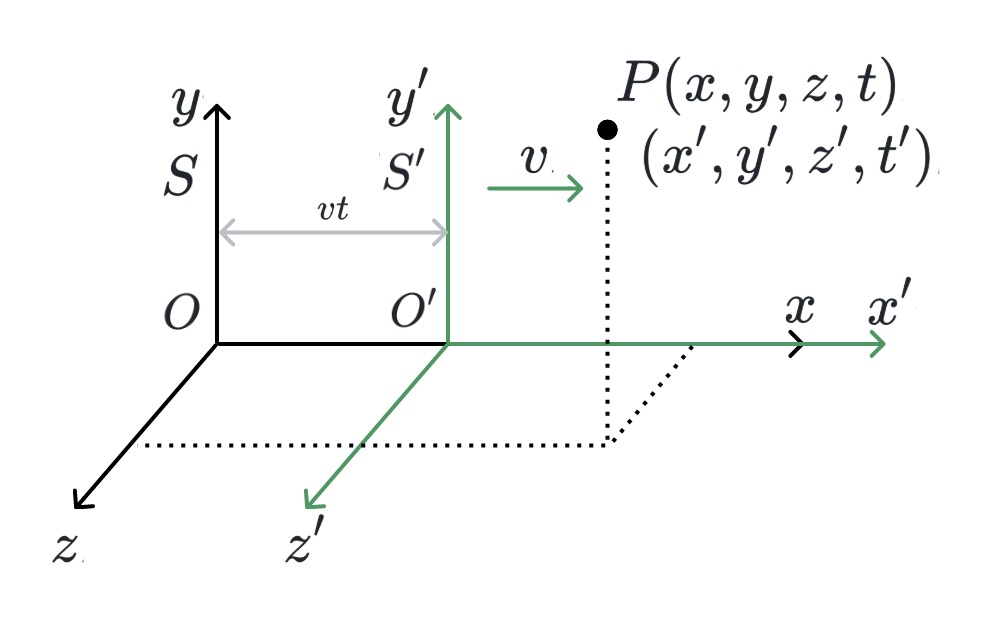
如图中有一时刻的事件\(P\),在\(S\)坐标系中坐标为\(P(x,y,z,t)\),在\(S'\)坐标系中坐标为\(P(x',y',z',t')\);
假设变换因子为\(γ\),则由\(S\)坐标系转到\(S'\)坐标系时\(X\)轴变化为:
公式一:\(x'=γ(x-vt)\)
由于相对性原理,不同惯性系中物理原理相同,所以\(S'\)转到\(S\)时\(X\)轴变化为:
公式二:\(x=γ(x'+vt')\)
以上公式一和二相乘得:
公式三:\(xx' = γ^2(x-vt)(x'+vt') = γ^2(xx'-vtx'+xvt'-v^2tt')\)
由于在\(Y\)轴和\(Z\)轴没有运动变化,所以:
\(y=y'\);\(z=z'\);
假设在时间为0时一光子从原点往\(X\)轴方向前进,由于光速在任何参考系中都为\(c\),所以经过一段时间之后,光子的坐标为\(x=ct\),\(x'=ct'\);
将此代入公式三得:
\(c^2tt'=γ^2(c^2tt'-vtct'+ctvt'-v^2tt')\)
\(tt'\)可约去,所以解得:
\(\bbox[#5DADE2,4px]{γ=}\sqrt{\frac{c^2}{c^2-v^2}}=\bbox[#5DADE2,4px]{\frac{1}{\sqrt{{1-({\frac{v}{c}})^2}}}}\)
将公式二代入公式一得:
\(x'=γ(γ(x'+vt')-vt)\)
\(t=\frac{-\frac{x'}γ+γx'+γvt'}{v} = \frac{γ(x'+vt'-\frac{x'}{γ^2})}{v}\)\(=γ(t'+\bbox[lightcyan]{\frac{γ^2x'-x'}{vγ^2}})\)
由于\(\bbox[lightcyan]{\frac{γ^2x'-x'}{vγ^2}} = x'\frac{\frac{1-(1-({\frac{v}{c}})^2)}{{1-({\frac{v}{c}})^2}}}{v\frac{1}{{1-({\frac{v}{c}})^2}}}=x'\frac{\frac{v^2}{c^2}}{v}=\bbox[lightcyan]{\frac{vx'}{c^2}}\)
所以:\(\bbox[#5DADE2,4px]{t=γ(t'+ {{vx'} \over c^2})}\)
所以整体的洛伦兹变换方程组为:
$$\bbox[lightgreen,4px]{\begin{cases} x=γ(x'+vt') = \frac{x'+vt'}{\sqrt{{1-({\frac{v}{c}})^2}}}\\ y=y' \\ z=z' \\ t= γ(t'+ {{vx'} \over c^2}) = \frac{t'+ {{vx'} \over c^2}}{\sqrt{{1-({\frac{v}{c}})^2}}} \end{cases}}$$
由于狭义相对性原理,只要将\(v\)换成\(-v\)即可得到另外一个变换式
$$\bbox[lightgreen,4px]{\begin{cases} x'=γ(x-vt) = \frac{x-vt}{\sqrt{{1-({\frac{v}{c}})^2}}}\\ y'=y \\ z'=z \\ t'= γ(t- {{vx} \over c^2}) = \frac{t- {{vx} \over c^2}}{\sqrt{{1-({\frac{v}{c}})^2}}} \end{cases}}$$
4. 速度的叠加
结论:在速度为\(v\)的飞船内有一个运动速度为\(u\)的物体,在静止的人看来这个物体的速度为\(\bbox[lightgreen,4px]{v_s = \frac{v+u}{1+\frac{uv}{c^2}}}。\)
假设在\(S'\)参考系中有一物体以速度\(u\)沿\(X\)轴向右运动;
当时间为0时,其位置位于原点,经过时间\(t'\)后,坐标为\((x',y',z',t')\),容易得出\(x'=ut'\);
我们计算在\(S\)坐标系中物体的速度,只需要计算\(\frac{x}{t}\)即可。
根据洛伦兹变换公式:
\({x' \over t'} = \frac{γ(x-vt)}{γ(t- {{vx} \over c^2})}=\frac{x-vt}{t- {{vx} \over c^2}}\)
而\(u={x' \over t'}\),所以\(u = \frac{x-vt}{t- {{vx} \over c^2}}\)
\(ut-\frac{uvx}{c^2} = x-vt\)
\(x(1+\frac{uv}{c^2}) = t(u+v)\)
\({x \over t} = \frac{v+u}{1+\frac{uv}{c^2}}\)
即叠加后的速度为\(v_s = \frac{v+u}{1+\frac{uv}{c^2}}\)。
5. 质增效应
结论:物体的质量随着运动速度的加快而增加,其转化公式为\(\bbox[lightgreen,4px]{m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}}\),其中\(m_0\)为静止质量;随着速度越来越接近光速,物体质量越来越大,速度达到光速时,质量将达到无穷大,这也就是任何有质量的物体速度无法达到光速的原因。
假设有一个动量\(P\),施加于\(S'\)坐标系中质量为\(m_0\)的物体,在\(S'\)参考系中,此物体的速度为\(u\),此时\(P=m_0u\);
根据速度叠加公式,在\(S\)坐标系看来,物体运动的速度增量\(v_s-v < u\);由此可以看出从\(S\)参考系中物体更难被推动(速度改变更小),所以可认为有速度的物体,其具有更大的质量(惯性质量)。
以下进行质增公式的推导:
假设在参考系\(S'\)中有一个质量为\(m_0\)的小球\(a'\),这个小球在\(S\)中的质量为\(m\),运动速度为\(v\);
同样在参考系\(S\)中也有一个质量为\(m_0\)的小球\(a\),这个小球在\(S'\)中的质量为\(m\),运动速度为\(-v\);
随后两球发生碰撞后并完全融合,相对于\(S\)参考系的速度为\(u\),相对于\(S'\)的速度为\(u'\);
在狭义相对论中,保留了动量守恒定律(动量为\(P=mv\)),所以对于\(S\)参考系,碰撞前后动量守恒:
\(mv=(m+m_0)u\)
同理,在\(S'\)参考系中,碰撞前后动量守恒:
\(m(-v) = (m+m_0)u'\)
由此可知\(u=-u'\)
由速度叠加公式可知\(u={u'+v \over 1+ {u'v \over c^2} }\)
将\(u=-u'\)代入得
\(u={u'+v \over 1+ {u'v \over c^2} }={-u+v \over 1- {uv \over c^2} }\),分母移到左边得:
\(u- {u^2v \over c^2} = -u+v\),全部右移,同时乘以\(\frac{v}{u^2}\)得:
\(({v \over u})^2 - 2\frac{v}{u}+\frac{v^2}{c^2} = 0\)
以\(\frac{v}{u}\)为整体并根据一元二次方程的解公式\(x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\),得:
\(\frac{v}{u}= \frac{2 \pm \sqrt{4-4\frac{v^2}{c^2}}}{2} = 1 \pm \sqrt{1-\frac{v^2}{c^2}}\)
由于\(v>u\)所以取结果\(\frac{v}{u} = 1+\sqrt{1-\frac{v^2}{c^2}}\)
代入\(mv=(m+m_0)u\)得:
\(m+m\sqrt{1-\frac{v^2}{c^2}} = m+m_0\)
故:\(\bbox[#5DADE2,4px]{m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}=γm_0}\)。
6. 质能公式推导
我们知道一个物体受外力作用后,动能就会增加,增加的能量表示为\(E_k=F·S\);
使用微积分思想,在非恒力\(F\)作用的情况下
\(E_k=\int_0^sFds\)
物体所受外力与加速度的关系是\(F=ma\),而加速度定义为\(\frac{dv}{dt}\);
另外由于\(m\)也是一个随着速度变化的量,所以我们借助动量的定义\(P=mv\)来进行;
这里力也可以看成是动量的变化率,即\(F=\frac{dp}{dt}=\frac{d(mv)}{dt}\);
而\(m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\),所以
\(E=\int_0^sFds=\int_0^s{\frac{dp}{dt}ds}=\int_0^s{\frac{d}{dt}\bigg(\frac{m_0v}{\sqrt{1-\frac{v^2}{c^2}}}\bigg)ds}\)
而\(ds=vdt\),所以上述式子
\(=\int_0^t{\frac{d}{dt}\bigg(\frac{m_0v}{\sqrt{1-\frac{v^2}{c^2}}}\bigg)v{dt}}=\int_0^v{v d\bigg(\frac{m_0v}{\sqrt{1-\frac{v^2}{c^2}}}\bigg) }\)
\(m_0\)是定值,可以提取到积分外面;
而\(d\bigg(\frac{v}{\sqrt{1-\frac{v^2}{c^2}}}\bigg)\)根据乘积法则\(\big(f(x)g(x)\big)' = fg'+gf'\)
令\(f=v\),\(g=(1-\frac{v^2}{c^2})^{-\frac{1}{2}}\)得:\(d\bigg(\frac{v}{\sqrt{1-\frac{v^2}{c^2}}}\bigg)=vd\Big((1-\frac{v^2}{c^2})^{-\frac{1}{2}}\Big)+(1-\frac{v^2}{c^2})^{-\frac{1}{2}}dv\)
由于\(d(x^n) = nx^{n-1}dx\),令\(x=1-\frac{v^2}{c^2}\)所以上述式子\(vd\Big((1-\frac{v^2}{c^2})^{-\frac{1}{2}}\Big)=v(-\frac{1}{2})(1-\frac{v^2}{c^2})^{-\frac{3}{2}}d(1-\frac{v^2}{c^2})\)
由于\(d(1-\frac{v^2}{c^2})=-\frac1{c^2}d(v^2)=-\frac1{c^2}·2vdv\)
\(v(-\frac{1}{2})(1-\frac{v^2}{c^2})^{-\frac{3}{2}}d(1-\frac{v^2}{c^2}) = v(-\frac{1}{2})(1-\frac{v^2}{c^2})^{-\frac{3}{2}}(-\frac1{c^2}·2vdv)=\frac{v^2}{c^2}(1-\frac{v^2}{c^2})^{-\frac{3}{2}}\)
代入:
\(\begin{align} \int_0^v{vd\bigg(\frac{m_0v}{\sqrt{1-\frac{v^2}{c^2}}}\bigg)} &= m_0\int_0^v{ v\Bigg( vd\Big((1-\frac{v^2}{c^2})^{-\frac{1}{2}}\Big)+(1-\frac{v^2}{c^2})^{-\frac{1}{2}}dv \Bigg) } \\ &=m_0\int_0^v{ \Bigg( \frac{ \frac{v^3}{c^2} } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } + \frac{v}{\sqrt{1-\frac{v^2}{c^2}}} \Bigg) dv }\\ &=m_0 \int_0^v{ \Bigg( \frac{ \frac{v^3}{c^2} } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } + \frac{v}{\sqrt{1-\frac{v^2}{c^2}}} \Bigg) dv }\\ &=m_0 \int_0^v{ \Bigg( \frac{ \frac{v^3}{c^2} + v- \frac{v^3}{c^2} } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } \Bigg) dv }\\ &=m_0 \int_0^v{ \frac{ vdv } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } }\\ &=m_0 \int_0^v{ \frac{ vdv } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } }\end{align}\)
我们可以使用换元法来求这个积分的值,本次变换用到了如下公式:
\(\sin^2x+\cos^2x=1\)
\(d(cos\ x)=-sin\ x\ dx\)
\(d(sin\ x)=cos\ x\ dx\)
令\(v=c\sin\theta\),则先求上述定积分在不定积分下的值
\(\begin{align} m_0 \int{ \frac{ vdv } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } }&=m_0\int\frac{c\sin\theta}{\Big(\sqrt{1-\sin\theta^2}\Big)^3}d(c\sin\theta)\\ &=m_0\int\frac{c^2\sin\theta\cos\theta}{\cos^3\theta}d\theta\\ &=m_0c^2\int {\sin\theta \cos^{-2}\theta } d\theta\end{align}\)
重新换元,令\(u=\cos \theta\),则\(du=-\sin\theta d\theta\),所以:
\(m_0c^2\int {\sin\theta \cos^{-2}\theta } d\theta\)\(=m_0c^2\int{ -\cos^{-2}\theta d(\cos\theta) } =-m_0c^2\int{ u^{-2}du }\)
由于\(\int{x^ndx} = (n+1)x^{n+1}+C\),所以
\(-m_0c^2\int{ u^{-2}du } =-m_0c^2(-2+1)u^{-2+1}+C =m_0c^2u^{-1}+C\)
因为\(u=\cos\theta\),而\(v=c\sin\theta\),所以
\(u=\cos\theta= \sqrt{1-\sin^2\theta}= \sqrt{1-\frac{(c\sin\theta)^2}{c^2}}= \sqrt{1-(\frac{v}{c})^2}\)
所以
\(m_0 \int{ \frac{ vdv } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } }=m_0c^2u^{-1}+C=m_0c^2\frac{1}{\sqrt{1-(\frac{v}{c})^2}}+C\)
所以
\(\begin{align}m_0 \int_0^v{ \frac{ vdv } { \Big(\sqrt{1-\frac{v^2}{c^2}}\Big)^3 } }&=m_0c^2\frac{1}{\sqrt{1-(\frac{v}{c})^2}}+C - (m_0c^2\frac{1}{\sqrt{1-(\frac{0}{c})^2}}+C)\\ &=\frac{m_0c^2}{\sqrt{1-(\frac{v}{c})^2}}- m_0c^2\end{align}\)
因为\(m=\frac{m_0}{\sqrt{1-(\frac{v}{c})^2}}\)
所以\(\bbox[lightgreen,4px]{E_k=mc^2-m_0c^2}\)。
终于,经过一系列的计算,我们终于得到了想要的式子;这个式子说明什么呢?物体由于外力作用所带来的动能增加等于质量的增加乘以光速的平方,也就是说能量的增加是质量增加与光速的平方相乘,能力与质量之间存在联系!这个联系就是
\[\bbox[lightgreen,4px]{E=mc^2}\]由于\(c^2\)是一个巨大的数字,也就是小小的质量里蕴含着巨大的能量,这也就是原子弹和氢弹的理论基础。
广义相对论
以笔者目前的物理和数学储备,不可能像狭义相对论一样从公式和数学出发去理解广义相对论。
所以只能从一些总结性的描述上去窥探广义相对论的精髓。
何为广义
广义相对论之所以是广义的,是因为他的适用范围由原来的惯性系推广到了非惯性系,也就是这一理论不再局限于静止或者匀速运动的情况,而是在非匀速场景和存在引力的场景也都适用。
等价性原理
处于加速状态的坐标系与处于均匀分布的引力场坐标系等价。
也就是说如果在太空中有一个以加速度\(g\)向上运行的车厢,你站在车厢内,无论通过何种物理实验,你都无法判断自己是在车厢中还是在地球上。
另外加速状态不但能产生引力场所具有的特性,而且还能抵消后者的影响。
如果在地球上自由落体,你将处于失重状态,与在太空中体验一致,这是因为你所受到的引力,与你的加速运动相抵消了。假如有一个地球上自由落体的车厢,你站在车内,则车厢可以看成一个惯性参考系。
广义相对论的推论
1. 光线弯曲
当光线经过引力场时,会沿着弯曲的路径进行传递,如同光线也受引力场吸引一样。
假设一个处于自由落体的车厢,根据等价原则,车厢内相当于一个惯性系。一束激光从车厢的左边射向右边,由于是惯性系,车厢内的人看到激光到达右边相同的位置,但在车厢外的人看来,由于加速度的存在,光线并不是做直线运动,而是曲线,向地心方向弯曲,也就是光线会受引力影响弯曲。
2. 引力红移
当光从一个质量巨大的物体附近逃逸时,它将损失一部分能量,它在光谱中的位置会向波长更长、能量更低的红色波段偏移,被称为红移。
在一个地球表面做自由落体的车厢1,从底部发出一束光线,在车厢1顶部的观察者由于多普勒效应,应该要观察到光线的蓝移(频率变高)。
在太空中处于静止的车厢2,也从底部发出一束光线,在车厢2顶部的观察者应该观察到光线的频率不变。
这与等价性原理中处于自由落体与处于静止状态等价相矛盾。所以处于引力场中的车厢1中的光线应该要受到红移以抵消蓝移的影响。
另外一个简单的解释是任何物质包括光线逃离引力场都需要消耗能量,而光的能量\(E=hv\),\(h\)为普朗克常数,\(E\)减少,则\(v\)减少,即频率降低,也就是发生了红移。
3. 引力是不平坦时空的结果
引力是不平坦时空的结果 ,物体总是沿着测地线运动,包括光线。
在广义相对论中,引力并不是真正的力,与离线心一样,他是一种等效力。在三维空间内看到的引力使光线发生弯曲,正是光线在四维时空中沿测地线运动的结果。

4. 引力越大,时间越慢
在引力场较强的地方,时间流速相对于引力场较弱的地方更慢。
由于地球上水平面的地方比高海拔的山上引力场更强,所以水平面上的时间比高山上的时间走得更慢(当然还要加上狭义相对论对于速度越快,时间越慢的影响)。
更极端地,黑洞有着超强的引力,这就导致了在黑洞周围的时间流速比外太空中时间流速慢很多,《星际穿越》里的米勒星球的1小时相当于地球7年的原因正是如此。
这一现象使用易懂的原理来解释比较难,有听说过这种解释的(笔者不置可否):引力越大,需要更大的转速以产生更强的离心力来逃脱引力,而更大的速度意味着时间越慢(狭义相对论),由此推导出引力越大,时间越慢。
实际上这一结论是由广义相对论引力场方程引出的:
\(R_{\mu\nu} - \frac{1}{2}Rg_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu}\)
其中,\(R_{\mu\nu}\) 是里奇张量,\(R\) 是里奇标量,\(g_{\mu\nu}\) 是度规张量,\(\Lambda\) 是宇宙学常数,\(G\) 是引力常数,\(c\) 是真空中的光速,\(T_{\mu\nu}\) 是能量 - 动量张量。
广义相对论认为,物质和能量会使时空弯曲,而引力就是这种时空弯曲的表现。在强引力场中,时空弯曲得更厉害。
时间的流逝本质上与时空的几何结构有关。当引力场变强时,时空的几何结构发生了更大程度的扭曲,导致时间的流逝就会变得更慢。
一些关于广义相对论的描述
-
空间和时间都不是绝对的,其形式和结构受物质和能量的影响。
-
物质和能量是时空弯曲程度的决定因素。
-
空间及其弯曲决定物质的运动方式。
与相对论相关的现象与概念
双生子佯谬
同时的相对性:火车实验
引力透镜/爱因斯坦环
水星近日点进动
宇宙微波背景辐射的各向同性
引力波
光锥
