Apr 21, 2023

发散地读一篇技术Blog

Posted in Tech

引言
开头
- Advent of Code
- Abs函数的性能讨论
循序渐进地深入
其它没有进行探讨的点
发散阅读

引言

最近在做的一个项目中遇到一个问题（其实也不算问题），需要对一个int64变量取绝对值，我想着math.Abs应该能用，发现这个参数支持的是float64，我对int64强制float64再转回来是否有问题没那么有信心，所以就放弃了这种方法，改用以下五行代码。

if configVersion > 0{
    return version > configVersion
}else{
    return version > -configVersion
}

但我并不是很甘心，是不是有什么其它的办法使用一行代码来解决呢，所以去网上搜索了一番，发现了这篇文章。

本来大概扫了一眼，基本拿到了我想要的结果，也就想着关掉页面了。但还是被它的一些内容吸引了，打算深究一下文档的详细内容，所以就有了本文。

开头

文章开头作者也是遇到了一样的问题，需要针对int64类型的Abs函数。类似地，作者也提出将int64转成float64后调用Abs函数，再转回来。但更进一步，作者接下来针对不同的方案进行了全面的分析和压测。

本文为发散地阅读一篇Blog，那肯定不会放过文章的开头中所包含的一些有意思的话题。

Advent of Code

首先作者引出问题的缘由是参加了一个叫做Advent of Code的挑战。Advent of Code (AoC)是Eric Wastl建立的一个网站，同时也是一年一度的一项编程竞赛的名称。

比赛时间是每年的12月1日至25日，每天北京时间下午一点网站上会准时放出当天的新题。每道题有两问，需要回答正确第一问后才能回答第二问。两问共用同一份输入文件。每一问的全球前一百名可以获得积分，从100到1依次递减。

比如文中提到的2017的Day 20的题目就是一个粒子群(Particle Swarm)问题。关于这个问题，里面还会涉及非常多的名词和概念，例如深度缓冲(z-buffering)、曼哈顿距离(Manhattan distance)、粒子群优化算法(PSO)等等。

Abs函数的性能讨论

作者还提到了关于math.Abs的性能讨论的golang邮件组帖子，里面讨论了各种Abs实现的性能差异，可以从中窥见Abs函数的历史版本以及go的历史版本中一些性能提升演化。值得注意的是Russ Cox也在帖子中回复了，并且指出了沿用至今的Abs写法。

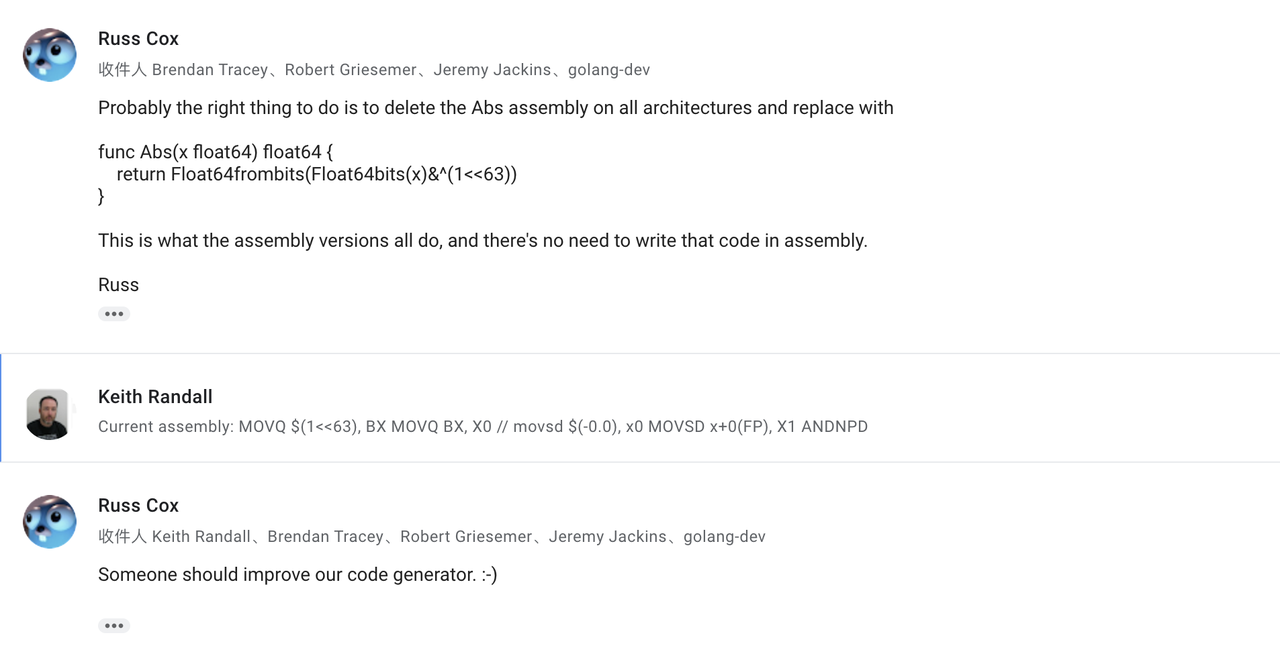
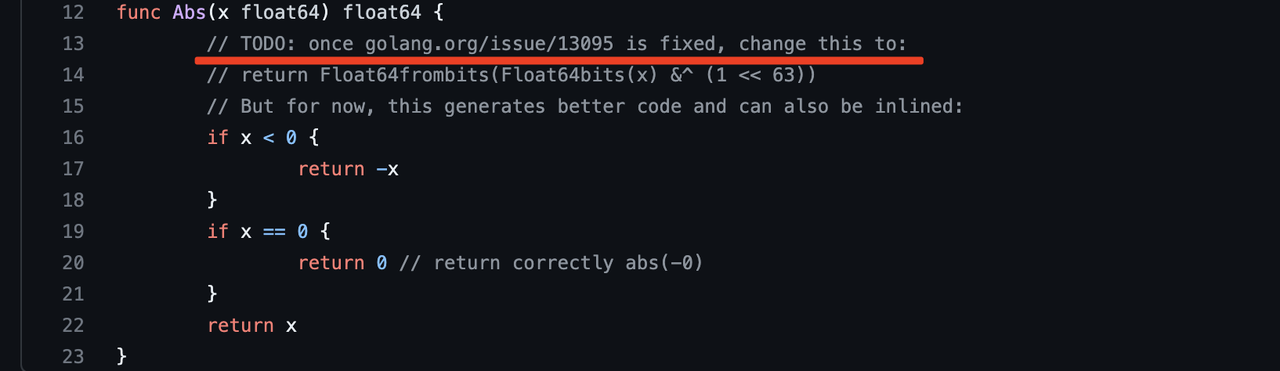
我也去扒了一下go1.5的源码，当时的math.Abs确实是用的switch来实现的，而在1.6.1的时候就换成了if来实现了。

而if和switch生成二进制之间的差异是什么，以及这个使用Float64frombits的bug又代表什么，可以继续发散深究下去(但我这由于精力问题就停止了:-)。

循序渐进地深入

文中的压测结果已经不太重要，实际上文中的压测结果你大概率不能进行复现，因为go版本经过迭代已经进行了大量的优化，这两种写法的差异性基本上已经磨平了。

我们更多地是顺着作者的思考，来发散地考虑文中都涉及到的一些知识点。现在从以下两种写法出发：

// if 分支法
func WithBranch(n int64) int64 {
        if n < 0 {
                return -n
        }
        return n
}

// 使用标准库
func WithStdLib(n int64) int64 {
        return int64(math.Abs(float64(n)))
}

简单测试带来的问题

直接写一个简单的Benchmark，使用固定输入执行压测：

func BenchmarkWithBranch(b *testing.B) {
        for n := 0; n < b.N; n++ {
                WithBranch(1)
        }
}

func BenchmarkWithStdLib(b *testing.B) {
        for n := 0; n < b.N; n++ {
                WithStdLib(1)
        }
}

这种压测结果并不能很好地反应出真实结果，因为CPU会对WithBranch中的函数进行分支预测，以加快指令的执行，如果将入参改成随机值的话，可以避免这种情况。

这里引出了一些问题，什么是分支预测呢？这可能要从指令流水线说起。借此简单巩固一下计算机组成原理(可能不严谨)。

指令流水线

以RISC为例，指令执行过程分成以下这些步骤

读取指令(Instruction fetch)
指令解码与读取寄存器(Instruction decode and register fetch)
执行(Execute)
存储器访问(Memory access)
写回寄存器(Register write back)

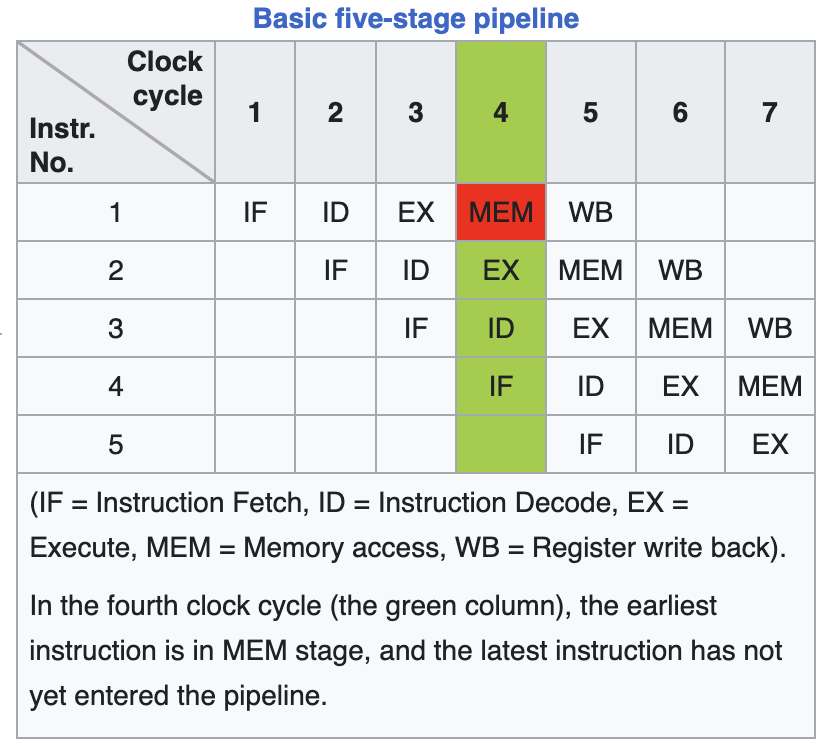
如果只是串行地执行这些步骤，则会耗费相当多的时间，所以现代CPU一般采用多层的流水线来加快这一处理过程，如下是一个5层流水线的示意图。可以看到随着流水线的增加，提高了指令执行的并行度。

分支预测

指令流水线有一个问题，就是现代程序中有很多的分支，你在执行当前指令的时候，其实并不知道后续要执行的指令是什么，他依赖于第一条指令的结果，所以这种情况下后面的指令就无法读取，需要等待之前的结果。这无疑增加了CPU空转的时长。

分支预测可以很大程度上缓解这一问题。以最简单的静态预测为例。一般分支有两条，静态预测方法是无脑加载第一条(紧跟着的指令)，如果前面的指令执行结果出来后发现不是执行第一条指令，则抛弃掉重新读取指令。

这中间还需要插入分支延迟间隙以获得上一指令执行结果。

现在CPU所用的分支预测基本上全部是动态预测，它是利用分支指令发生转移的历史来进行预测，并根据实际执行情况动态调整预测位，准确率可达90%。

随机函数生成器的选择

解决之前简单参数所带来的问题，引入了随机参数，这就用到了随机数生成器。在go中有math/rand库的随机数生成器可选(伪随机)，但这里作者使用了xorshift这一随机函数生成器，代码比基础库中的简单很多，性能应该也快不少，没有做实际的验证。有兴趣地同学可以研究一下xorshift的论文，对比一下基础库中生成方式与此的不同点。

另外真随机生成器crypto/rand的生成原理，有兴趣也可以了解一下。

float64和int64强转所带来的截断问题

func TestRand(t *testing.T){
        fmt.Println(WithBranch(-9223372036854775807),WithStdLib(-9223372036854775807))
        // 输出 9223372036854775807 -9223372036854775808
}

看以上的例子，使用StdLib完全出现了错误的结果，这是由于在math.Abs转化后的float64超过了int64的范围，所以强转后溢出变成负数了。

强转(conversions)

首先，为什么float64和int64可以进行强转呢？我在Go Specification中看到了对应的规则，但并没有搜索到转换的规则是什么（只看到int64到float64的转化，反之没有看到，待指证）。

A non-constant value x can be converted to type T in any of these cases:

x is assignable to T.

ignoring struct tags (see below), x’s type and T are not type parameters but have identical underlying types.

ignoring struct tags (see below), x’s type and T are pointer types that are not named types, and their pointer base types are not type parameters but have identical underlying types.

x’s type and T are both integer or floating point types.

x’s type and T are both complex types.

x is an integer or a slice of bytes or runes and T is a string type.

x is a string and T is a slice of bytes or runes.

x is a slice, T is an array or a pointer to an array, and the slice and array types have identical element types.

Int64到Float64的转化：

T is a floating-point type and x can be rounded to T’s precision without overflow. Rounding uses IEEE 754 round-to-even rules but with an IEEE negative zero further simplified to an unsigned zero. Note that constant values never result in an IEEE negative zero, NaN, or infinity.

关于强转这块还涉及到数值修约方式(Rounding)，以及CPU对于待定计算过程中的优化，如FMA等。

IEEE 754

float类型的保存格式都采用的IEEE 754标准，我们再一起再回顾一下其存储格式。

格式说明

对浮点数进行存储，需要先进行规范化。例如1789，规范化之后就是1.789*10^3，而对于二进制来说，个位数总是为1，所以存储时会忽略这块的数值。

以float64类型为例，如上图，这8个字节分成三个部分，第一个bit位代表符号(sign)，紧接着是指数位(exponent)，总共有11位，最后52位是小数部分(fraction)。

符号位：与int64一样，0表示正数，1表示负数；

指数位：即科学计数法中的指数，只是这里的底不是10而是2。注意指数位是无符号类型的，所以其范围是0~2047。但对于指数来说有正有负，这里涉及到偏置（Bias）值，Bias 等于 2^(k-1)-1，对于float64即1023，所以指数位的范围为-1023~1024；

小数位：小数位就是小数位，是排除掉个位的1之后小数点右边的数值。

举例说明

以-1234.70703125为例，我们一步一步转成float64：

首先转化成二进制，先是整数部分，不断除2取余，结果为10011010010；
再取小数部分，转化为二进制，对小数部分不断乘2，取个位值，结果为：10110101；
规范化科学计数法-1.001101001010110101 x 2^10，至此，可以确定小数部分值为0011010010101101010000000000000000000000000000000000；
确定指数部分，现在指数为10，10+Bias(1023) = 1033，二进制为10000001001；
所以整体的数值为1100000010010011010010101101010000000000000000000000000000000000，红色为符号，绿色为指数，紫色为小数部分。


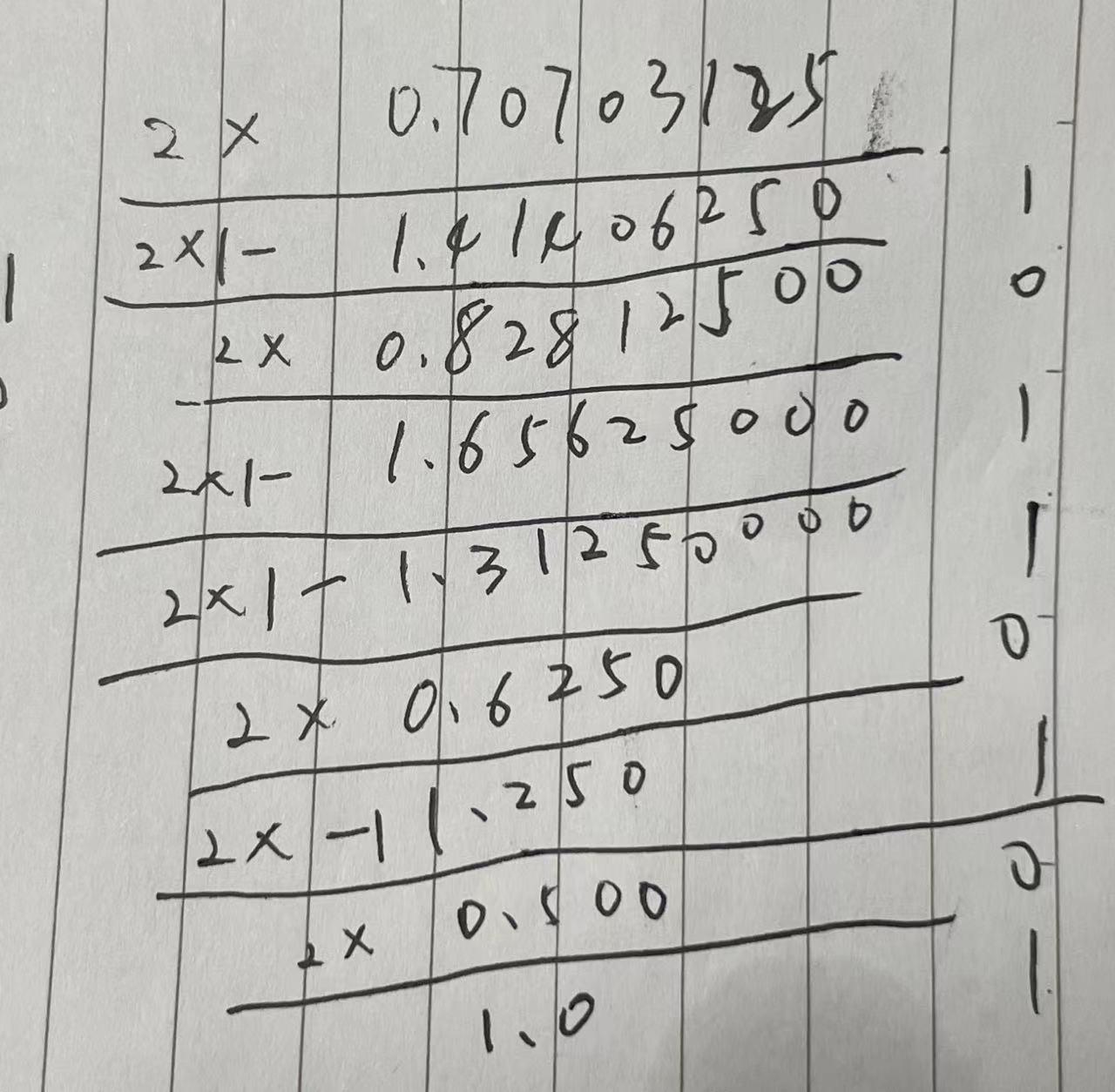整数部分转化过程	小数部分转化过程

验证一下

    fmt.Printf("%b\n", math.Float64bits(-1234.70703125))
    // 打印：1100000010010011010010101101010000000000000000000000000000000000

使用补码计算绝对值

作者进一步使用了补码的思路来计算绝值，我们还是顺着这些概念一步一步理解如何达成目标的。

补码( two’s complement arithmetic )

众所周知计算机中的int类型是通过补码存储的，所以我们不能仅通过将最高的符号位转成0来求Abs。

计算补码非常简单，正数为本身，负数取反加1即可，假设一个int8类型的值为-9，其正数的二进制表示为00001001，对其取反，11110110，再对其加1，11110111，这就是最终保存的结果。验证如下：

    k := int8(-9)
    fmt.Printf("%b\n", *(*uint8)(unsafe.Pointer(&k)))
    // 输出 11110111

这里抛出一个问题：为什么要用补码呢？

使用补码计算int的绝对值

我们先看一下流程：假设我们要取x的绝对值，x为int64，可正可负，则过程如下：

将x右移63位得到y，即y := x >> 63；
计算(x XOR y) -y 即可得到最终结果。

我们分两种情况讨论这个过程的正确性：

x为正数	1. 首先x往右移63位，将得到一个全0的二进制数，也就是0； 2. x与全0的y取异或结果还是x，所以`x XOR y = x`； 3. 再减去0，自然还是x了。
x为负数	1. 首先x往右移63位，将得到一个全1的二进制数，也就是-1； 2. x与全1的y取异或相当于取反； 3. -y为1，所以取反+1即可得到负数的绝对值。

使用汇编编写

go支持编写原生汇编代码，将原文件命名成.s后缀即可，然后在go文件中声明对应的函数，如刚才的计算过程函数表示为：

// abs_amd64.s
TEXT ·WithASM(SB),$0
  MOVQ    n+0(FP), AX     // copy input to AX
  MOVQ    AX, CX          // y ← x
  SARQ    $63, CX         // y ← y ⟫ 63
  XORQ    CX, AX          // x ← x ⨁ y
  SUBQ    CX, AX          // x ← x - y
  MOVQ    AX, ret+8(FP)   // copy result to return value
  RET