笔者对于函数式编程纯属完全的门外汉,但一直想窥觑其一隅。故开坑精读《Hashkell函数式编程入门》以求入门,以此笔记为据。以至于此文大量初级知识,博君见笑。
环境的准备
安装
使用书中推荐的GHC(The Glasgow Haskell Compiler)来做为编译器,其提供了一个可交互的shell(GHCi)来进行类似解释执行的功能,可以方便我们的调试。
➜ ~ brew install ghc
➜ ~ ghci
GHCi, version 8.6.5: http://www.haskell.org/ghc/ :? for help
Prelude>
出现提示后(Prelude是GHCi运行时一个默认的环境 ,定义了很多类型和函数的库)就可以在上面编写hashkell语句来运行了。不过在此之前,介绍GHCi提供的常用命令。
常用命令
命令以冒号开头,各命令用法如下(都省掉了前导的冒号):
load:简写为l,导入指定文件
reload:简写为r,用来重新导入修改后的文件
cd:切换工作路径
edit:编辑当前导入的文件,使用环境变量EDITOR来指定编辑器
module:简写为m,导入一个库,可以使用:m +[module]或者:m -[module]来添加了移除模块
quit: 退出
type: 简写为t,查看变量的类型
info: 简写为i,查看运算符或者函数的信息,如优先级,结合性,定义位置等
kind: 简写为k,查看类型的类型
?:帮助
基本语句示例
在GHCi上已经可以进行一些基本的操作了:
-- 简单运算
Prelude> 4+6*7/3
18.0
-- 三角函数运算与pi定义
Prelude> log 2.71828
0.999999327347282
Prelude> sin(pi/3)/cos(pi/3)
1.7320508075688767
-- 布尔类型
Prelude> True && False
False
Prelude> True || False
True
-- 列表容器,以及对其求和、积
Prelude> [1..4]
[1,2,3,4]
Prelude> sum [1..4]
10
Prelude> product [1..4]
24
-- it指向上一次结果
Prelude> it+2
26
使用hs和lhs文件
如下helloworld.hs:
-- 这是我的第一个程序
{- 这是多行注释 -}
main = putStrLn "Hello world"
hs文件代码要顶头写,单行注释使用--,多行注释使用{-和-}来处理。
以上的程序可以使用ghc直接编译成可执行文件,也可以使用runghc程序来直接运行:
➜ ~ ghc helloworld.hs
[1 of 1] Compiling Main ( helloworld.hs, helloworld.o )
Linking helloworld ...
➜ ~ ./helloworld
Hello world
➜ ~ runghc helloworld.hs
Hello world
而lhs文件是用来生成文档的,所以会有各种各样的格式来生成精美的文档,如下helloworld.lhs
这是一行注释,代码行以空格或者>开始
注释与代码间一定要有空行
> main = putStrLn "Hello world"
类型系统和函数
Haskell是强类型语言,可以ghci中输入:t来查看变量的类型。
布尔类型Bool
只有True和False两个值,提供的与或非运算符分别是&& || not,例子如下:
Prelude> :t True
True :: Bool
Prelude> True && False
False
Prelude> True || False
True
Prelude> not True
False
字符型
单引号表示,可以使用转义字符,例子如下:
Prelude> :t 'c'
'c' :: Char
Prelude> '\100'
'd'
整数
整数主要有有符号整数(Int)、无符号整数(Word)、任意精度整数(Integer)。还有其它的如Int8,Int16,Word8,Word16这样的类型。
Int
范围与操作系统相关,64位机器表示的范围为-2^63 ~ 2^63-1,所以输入2^64::Int返回值为0。需要使用::Int 指定类型,因为默认会处理成任意精度整数。
Prelude> 2^64::Int
0
Prelude> :t it
it :: Int
Word
Word是Data.Word库中带的,所以需要导入外部库。其在64位机上的范围为0 ~ 2^64-1。
Prelude> :m +Data.Word
Prelude Data.Word> -1::Word
<interactive>:31:2: warning: [-Woverflowed-literals]
Literal -1 is out of the Word range 0..18446744073709551615
18446744073709551615
Prelude Data.Word> :t it
it :: Word
Prelude Data.Word> :m -Data.Word
Integer
Haskell可以表示任意精度整数类型,它会自动进行类型转化:
Prelude> product [1..100]
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
小数和有理数
浮点小数分成Float和Double,与其它语言类似,不同的是Haskell多了有理数类型Rational,使用两个任意精度的整数来表示一个小数。
Prelude> :t pi
pi :: Floating a => a
Prelude> pi::Float
3.1415927
Prelude> pi::Double
3.141592653589793
Prelude> :t it
it :: Double
Prelude> 1/3::Rational
1 % 3
Prelude> 0.2::Rational
1 % 5
字符串类型String
String类型其实为[Char]
Prelude> ['H', 'e' ,'l', 'l', 'o']
"Hello"
Prelude> :t ['H', 'e' ,'l', 'l', 'o']
['H', 'e' ,'l', 'l', 'o'] :: [Char]
Prelude> :t "Hello"
"Hello" :: [Char]
Prelude> "Hello"::String
"Hello"
Prelude> :t it
it :: String
元组类型
元组是包含多个元件的一组数据,例如(“Chai”, 1990, 02, 27, “男”)这样。
如果只有两个元件,称之为二元组,它有两个重要的函数fst获取第一个元件,snd获取第二个元件。
Prelude> :t ("Chai", 1990, 02, 27, "男")
("Chai", 1990, 02, 27, "男")
:: (Num b, Num c, Num d) => ([Char], b, c, d, [Char])
Prelude> fst (1,2)
1
Prelude> snd (1,2)
2
列表类型 list
列表定义:
a. 它可以是一个空列表,即[]
b. 它可以是一个元素与另一个列表的结合,即x:xs,x为一个元素,xs是一个列表
Prelude> 1:[2..4]
[1,2,3,4]
Prelude> :t 1:[2,3]
1:[2,3] :: Num a => [a]
Prelude> :t [(+),(-)]
[(+),(-)] :: Num a => [a -> a -> a]
注意:列表可以存储列表,但是一个列表里的类型一定是一样的。
函数类型
即参数到结果的映射:T1 -> T2;
如果T1或者T2为函数,则称之为高阶函数(high order function)。
柯里化函数(curried function)
一个函数如果有多个参数时,参数可以依次输入,如果参数不足时,返回一个函数做为结果。
如定义add支持两个参数,结果为两个参数相加。
Prelude> let add x y = x + y::Int
Prelude> add 1 2
3
Prelude> :t add 1
add 1 :: Int -> Int
如果将两个参数视为二元组,则相当于只接收一个参数,则称这个接收二元组的函数为非柯里化(uncurry)函数,过程为非柯里化。相反,从非柯里化函数想到对应的柯里化函数称之为柯里化(curry)。
互相转化的例子
Prelude> let add' (x,y) = x + y::Int
Prelude> add' (1,2)
3
Prelude> :t curry
curry :: ((a, b) -> c) -> a -> b -> c
Prelude> :t add'
add' :: (Int, Int) -> Int
Prelude> :t curry add'
curry add' :: Int -> Int -> Int
Prelude> :t add
add :: Int -> Int -> Int
Prelude> :t uncurry add
uncurry add :: (Int, Int) -> Int
多态函数
函数的参数类型可以是多个类型的函数称之为多态函数,例如fst,length,head等函数。
Prelude> fst (1,2)
1
Prelude> fst (False, True)
False
Prelude> fst ([1], [2])
[1]
Prelude> length [1,2,3]
3
Prelude> length "hello"
5
Prelude> :t fst
fst :: (a, b) -> a
Prelude> :t length
length :: Foldable t => t a -> Int
Prelude> head [1..3]
1
Prelude> :t head
head :: [a] -> a
Prelude> zip [1,2,3] [4,5,6]
[(1,4),(2,5),(3,6)]
Prelude> :t zip
zip :: [a] -> [b] -> [(a, b)]
重载类型函数
如之前定义的add函数,只支持Int类型的操作。在Haskell中支持类型类,如abs的定义abs :: Num a => a -> a,其中=>为类型类限定符号,表示a类型必须限定在一个名为Num的类型类中,这样的函数称之为重载函数。
类型的别名
使用type关键字可以将复杂的类型替换成简单的名字。
Prelude> type RGB = (Int, Int, Int)
Prelude> type Picture = [[RGB]]
Prelude> (1,2,3)::RGB
(1,2,3)
类型类
将类型进行归类,称之为类型类。
相等类型类 Eq
实现了Eq类型类的类型可以判断是否相等,即(==)。函数的类型为(==) :: Eq a => a -> a -> Bool,表示(==)函数是参数限定为类型类Eq,支持两个参数,并且返回Bool的函数。
Eq类型类还可以判断是否不相等(/=):
Prelude> (==) 1 1
True
Prelude> :t (==)
(==) :: Eq a => a -> a -> Bool
Prelude> :t (/=)
(/=) :: Eq a => a -> a -> Bool
有序类型类Ord
可比较大小的类型:
Prelude> :t (>)
(>) :: Ord a => a -> a -> Bool
Prelude> :t (>=)
(>=) :: Ord a => a -> a -> Bool
Prelude> :t (<)
(<) :: Ord a => a -> a -> Bool
枚举类型类 Emum
例如整数列表的形式[1..10],正是由于整型为枚举类型,所以可以对1到10之间的数进行枚举,字符串也是枚举类型。
枚举类型支持succ取后一个元素和pred取前一个元素的两个函数。
Prelude> [1..10]
[1,2,3,4,5,6,7,8,9,10]
Prelude> ['a'..'z']
"abcdefghijklmnopqrstuvwxyz"
Prelude> succ 10
11
Prelude> pred 'M'
'L'
有界类型类 Bounded
有界类型支持获取最大值和最小值:
Prelude> maxBound::Bool
True
Prelude> maxBound::Int
9223372036854775807
Prelude> maxBound::Char
'\1114111'
Prelude> minBound::Char
'\NUL'
数字类型类 Num
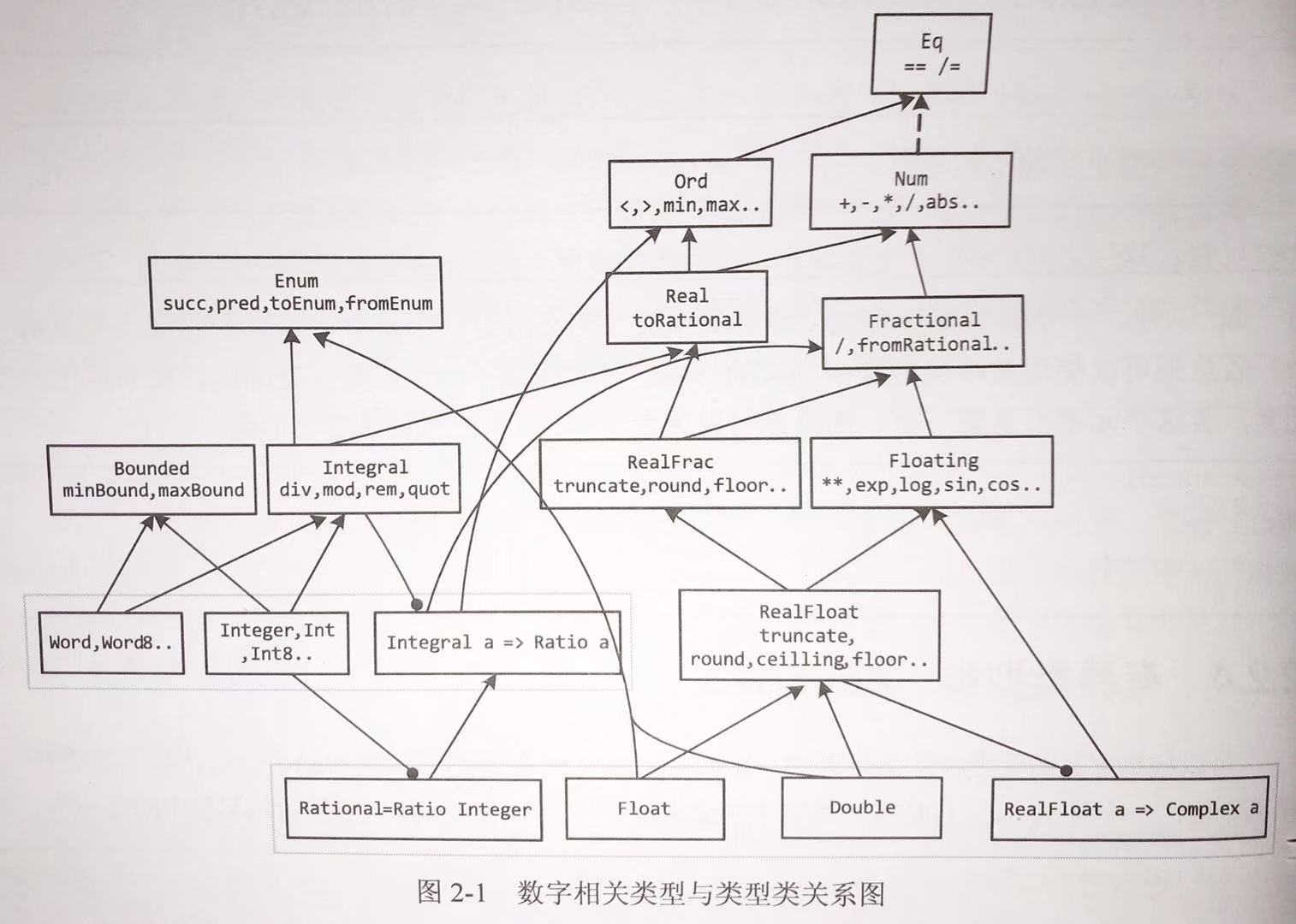
数字类型类有复杂的细分,对于类型来说如之前已经看到的Rational(有理数),Int,Float,Double,还有一些类型如Complex类型,是需要依赖另外一个类型,例如 Complex Float,Complex Double等。
这些类型都属于Num类,在Num类之下,还有Floating,Fractional等等。
如下图
Prelude> :m Data.Complex
Prelude Data.Complex> (5:+5)+(1:+1)
6.0 :+ 6.0
Prelude Data.Complex> :t it
it :: RealFloat a => Complex a
Prelude Data.Complex> [1.0,1.5..3]
[1.0,1.5,2.0,2.5,3.0]
Prelude Data.Complex> [1.0,1.5..3.1]
[1.0,1.5,2.0,2.5,3.0]
Prelude Data.Complex> pred 0.1
-0.9
浮点数的枚举是通过指定间隔来实现,默认的间隔为1。
可显示类型类 Show
Show类体现在可以在终端输出显示,如果没有实现Show类,则会报错。
Haskell中的函数
变量定值
Haskell中的变量值在绑定之后就不能改变了,只能使用。
如下的values.hs文件,编译时会报错:
a = "2"
a = "3"
main = putStrLn a
➜ runghc values.hs
values.hs:2:1: error:
Multiple declarations of ‘a’
Declared at: values.hs:1:1
values.hs:2:1
|
2 | a = "3"
| ^
函数思想
对于haskell来说,运算符也是函数,是一个二元函数,如果只给出一个参数,则返回一个一元函数,这种没有给出所有函数的应用称之为不完全应用(偏函数调用)。
Prelude> :t (+)
(+) :: Num a => a -> a -> a
Prelude> :t (5+)
(5+) :: Num a => a -> a
函数定义
函数名 :: 参数1的类型 -> 参数2的类型 -> … -> 结果类型
函数名 参数1 参数2 … = 函数体
例子
add :: Int -> Int -> Int
add a b = a+b
其中::用来指定函数的类型,表示add这个函数是接收两个Int类型的参数,返回Int类型。
函数的类型也可以通过编译器的类型预测来处理,不需要手动显示,例如:
Prelude> sub a b = a-b
Prelude> :t sub
sub :: Num a => a -> a -> a
如果限定的参数类型为类型类,需要使用类型限定的方式来定义:
add :: Num a => a -> a -> a
add a b = a+b
多个类型限定时,表示为如下两种形式:
sub :: (Show a, Num a) => a -> a -> a
sub a b = a - b
mul :: Show a => Num a => a -> a -> a
mul a b = a * b
λ表达式
另外一种定义函数的形式,即λ表达式形式:
函数类型 :: 参数的类型1 -> 参数的类型2 -> … -> 结果类型
函数名 = \参数1 -> \参数2 -> … -> 函数体
第二行中的参数之间的箭头可以省略,例如:
and :: (Eq a) => a -> a -> Bool
and = \x -> \y -> x == y
not :: (Eq a) => a -> a -> Bool
not = \x y -> x /= y
α替换(α-conversion)
α替换是指在命名不冲突的前提下可以将函数的参数重新命名。
例如 \x -> \y -> x + y经过α替换将x替换成a后\a->\y->a+y,这两个函数定义是等价的。
β简化(β-reduction)
β简化是指将参数应用于函数体,例如之前的函数定义and可以通过应用参数x和y通过β简化来定义成普通的函数定义形式:
and x y
= (\x->\y->x==y) x y
= (\y -> x == y) y
= x == y
又如:
(\x -> \y -> x y) (abs) (-5)
= (\y -> abs y) (-5)
= abs (-5)
= 5
η简化(η-reduction)
η简化可以消除冗余的λ表达式,例如:
f :: Num a => a -> a -> a
f = \y->\x->(+) x y
这个f函数其实就是(+),所以可以使用η简化为f = (+)。
注意η简化受单一同态约束影响,所以一般都要标明函数类型的签名。
单一同态限制(Monomorphism restriction)
在未明确指定类型的函数中,单一同态限制规则有可能会使用默认的类型。其作用是避免重复计算和消除类型歧义。
在GHCi中默认是关闭的,但编译的程序默认是开启的。
在GHCi中,可以按如下例子来测试:
Prelude> :set -XMonomorphismRestriction
Prelude> f = (+)
Prelude> f 1 1.0
<interactive>:6:5: error:
• No instance for (Fractional Integer)
arising from the literal ‘1.0’
• In the second argument of ‘f’, namely ‘1.0’
In the expression: f 1 1.0
In an equation for ‘it’: it = f 1 1.0
Prelude> :t f
f :: Integer -> Integer -> Integer
参数绑定
可以使用let ... in或者 where 语法,在函数体内多次用到某个值时,可以进行简化,例如海伦公式中的p:
heronSFormula :: Floating a => a-> a -> a ->a
heronSFormula a b c = sqrt(p*(p-a)*(p-b)*(p-c)) where p = (a+b+c)/2
heronSFormula' :: Floating a => a-> a -> a ->a
heronSFormula' a b c = let p = (a+b+c)/2 in sqrt(p*(p-a)*(p-b)*(p-c))
表达式
条件表达式 if…then…else
isTwo :: Int -> Bool
isTwo x = if x==2 then True else False
条件表达式可以理解为一个函数或者运算法,类型为Bool->a->a->a,称之为混合位置运算符。
注意条件表达式的else不能省略,而且then和else返回的数据类型要一致。
情况分析表达式 case of
daysOfMonth :: Int -> Int
daysOfMonth x = case x of
1 -> 31
2 -> 28
3 -> 31
4 -> 30
_ -> error "invalid month"
其中_表示default,多个匹配时返回第一个。
守卫表达式
myAbs :: (Num a, Ord a) => a -> a
myAbs n | n > 0 = n
| otherwise = -n
|符号后面跟着条件,上面的otherwise永远为true,多个匹配时返回第一个。
模式匹配
即枚举出所有的情况,其实与case of是等价的:
daysOfMonth' :: Int -> Int
daysOfMonth' 1 = 31
daysOfMonth' 2 = 28
daysOfMonth' 3 = 31
daysOfMonth' 4 = 30
daysOfMonth' _ = error "invalid month"
另外看一下Prelude库里head的定义
head :: [a] -> a
head (x:_) = x
head [] = error "Prelude.head: empty list"
运算符
运算符和函数其实是等价的,只是参数放置的位置不一样,完全可以把运算符放在前面如(+) 5 3,或者把函数放在中间5 `add` 3。
*Main> (+) 3 5
8
*Main> 3 `add` 5
8
运算符有0~9一共10个优先级,结合性上又分成左结合性、无结合性、右结合性。函数也可以理解为运算符,具有最高的优先级,左结合性,所以函数的参数一般需要加括号。
常用的运算符
(!!) 从列表中取出第n个元素(从0开始),例如 [1,2,3,4] !! 3
(.) 复合函数运算符
(^)、(^^)、(**)这三个都是乘方函数,获取是参数类型不同,前两个只能是整型指数,而(**)的底和指数都是Floating类型类
mod和rem是取余,quot和div是求商,但在计算负数时,结果会有些不同
(:) 将元素添加进列表,例如1:[2,3,4]结果为[1,2,3,4]
(++) 列表连接符号,将两个列表合并成一个列表[1,2] ++ [3,4]结果为[1,2,3,4]
($) 定义为f $ x = f x,最低优先级和右结合性,所以这个运算符是用来改变优先级和结合性的,可以替代括号的部分功能,例如(+) 2 $ (-) 5 3等价于(+) 2 ((-) 5 3 )
($!)、($!!)与seq为惰性求值相关的运算符
Haskell中允许自定义运算符,有三个指令infixl为左结合性,infixr为右结合性,infix为无结合性,后跟优先级及运算符名称。
例如php中的宇宙飞船操作符<=>
-- defind <=>
infix 5 <=>
(<=>) :: Ord a => a -> a -> Int
(<=>) x y | x > y = 1
| x < y = -1
| otherwise = 0
基于布尔值的函数
import与module
Haskell代码的第一行可以声明一些编码器参数,接着以module xxx where的格式定义模块的名字及导出的函数或者类型。
例如 module Test (f1,f2) where表示只导出这个包里的f1和f2,其它的都是私有的。如果不想导出任何方法,则使用module Test () where,而如果要导出所有方法,使用module Test where即可。
import可以导入模块,如import Test (f1)表示导入Test的f1方法;如果要导入除了某些函数外的其它所有函数,可以使用import Prelude hiding (xx,xx);需要换名称时,使用import qualified Test as T。
简易布尔值的函数
bool.hs
import Prelude hiding ((/=),(==),not,and,or,(&&),(||))
-- 重新定义
(==),(/=),and,or,(&&),(||),xor :: Bool->Bool->Bool
(==) True True = True
(==) False False = True
(==) _ _ = False
(/=) x y | x == y = False
| otherwise = True
not :: Bool -> Bool
not x = x == False
and True x = x
and _ _ = False
or False x = x
or _ _ = True
(&&) = and
(||) = or
xor = (/=)
infix 4 ==
infix 4 /=
infixl 3 &&
infixl 2 ||
半加法器和全加法器的实现
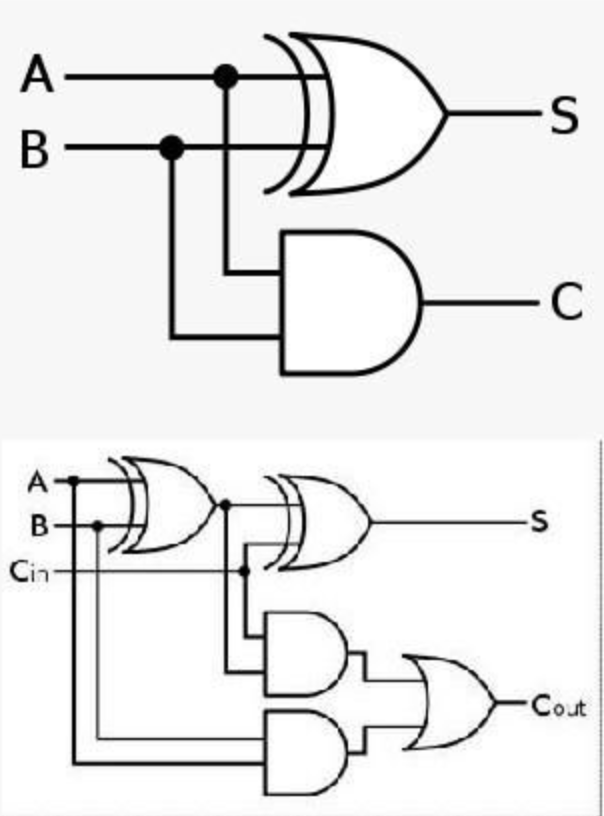
-- 半加法器,即不含有进位的加法器
halfAdd :: Bool -> Bool -> (Bool, Bool)
halfAdd a b = (a /= b, a && b)
-- 全加法器,包含有进位
fullAdd :: Bool -> Bool -> Bool -> (Bool, Bool)
-- fullAdd a b c = (,(a/=b) /= c)
fullAdd a b c = let (s1, c1) = halfAdd a b in
let (s2, c2) = halfAdd s1 c in (s2, c1 || c2)
库函数及其应用
Prelude常用库函数
id:恒值函数,返回给定的任何值,可以做为占位使用,例如可以与const联合,返回第二个参数的值的函数const id
const:常值函数,类型为const::a->b->a,即给定两个元素,返回第一个
flip:参数反转函数,类型为(a->b-c) ->b->a->c,对于一个接收两个参数的函数,如果要返回只接收第一个参数的函数,可以使用flip
error:错误函数,类型为error::String -> a,会抛出异常
undefined:定义是undefined = error "Prelude; undefined",其实是一个异常,可以在调试或者测试时占位
min、max:返回两个参数中最小、最大的那个
even、odd:判断一个数是否为偶数、奇数
-- 先计算const id 5 返回id函数,然后id 4返回4
Prelude> const id 5 4
4
Prelude> :t (:)
(:) :: a -> [a] -> [a]
Prelude> :t flip (:)
flip (:) :: [a] -> a -> [a]
Prelude> flip const True False
False
Prelude> error "should not here"
*** Exception: should not here
CallStack (from HasCallStack):
error, called at <interactive>:16:1 in interactive:Ghci5
Prelude> undefined
*** Exception: Prelude.undefined
CallStack (from HasCallStack):
error, called at libraries/base/GHC/Err.hs:78:14 in base:GHC.Err
undefined, called at <interactive>:19:1 in interactive:Ghci6
Prelude> :type min
min :: Ord a => a -> a -> a
Prelude> min True False
False
Prelude> max 10 29
29
列表相关函数
null:判定一个列表是否为空null::[a]->Bool
length:列表长度,注意返回的类型为Int,所以如果计算时需求Fractional类型类时,需要使用fromIntegral函数转成小数,或者使用Data.List里的genericLength函数返回Num类型的小数
import Data.List (genericLength)
avg,avg1,avg2 :: (Floating a) => [a] -> a
-- avg xs = sum xs / length xs 不能这样写,因为sum和length类型不匹配
avg xs = sum xs / fromIntegral (length xs)
avg1 xs = sum xs / (fromIntegral $ length xs)
avg2 xs = sum xs / genericLength xs
(!!): 运算符,取列表的第n个元素,注意越界异常
reverse:将一个列表倒过来
head、last:取第一个元素、最后一个元素,空列表报错
init、tail:将列表的最后一个、第一个元素去掉,空列表报错
map:将列表里的每一个元素按函数映射到另外一个元素组成列表,例如将每一个元素平方加1:map (\x->x^2+1) [1..10],这中间用到了λ匿名函数。map是一个高阶函数
filter:使用指定函数过滤掉列表中不满足要求的元素,类型为filter :: (a -> Bool) -> [a] -> [a]
take、drop:取列表的前n个元素,或者去掉n个元素,例如take 5 [1..]将返回[1,2,3,4,5],[1..]将是一个无限的列表,这个程序能运行与惰性求值相关
span、break:用于分割列表,span会在遇到第一个不满足条件元素时停止,从这里分割,而break正好相反,在遇到满足条件时才分割
takeWhile、dropWhile:与take和drop类似,只是第一个参数为一个a -> Bool函数
splitAt:按位置分割列表
repeat、replicate:repeat组成无限的给定元素列表,如repeat 10等价于[10,10..],replicate可以指定复制次数
any、all:any判断列表中是否有指定条件的元素,而all判断列表里的所有元素是否都满足指定条件
elem、notElem:elem判断元素是否存在于列表中,而notElem判断元素是否不存在于列表中,元素必须实现Eq类型类才行
iterate、until:iterate会使用第一个函数参数,迭代第二个元素无数次生成一个无限列表,例如iterate (*2) 1生成一个等比数列,而until添加了一个停止条件函数并返回第一个满足条件的值
zip、unzip:zip可以将两个列表合并成一个二元组的列表,例如zip [1,3,5] [2,4,6]结果为[(1,2),(3,4),(5,6)]多余的元素将被忽略,而unzip正好相反。可以使用zip3和unzip3来操作三个列表和三元组
zipWith:使用一个函数合并数组,而不是直接合并成二元组,zipWith3提供了三个列表的操作
concat:将列表中的列表连接起来变成一个列表
comcatMap:先将列表里的元素按函数map完成后再调用concat,类型为concatMap :: Foldable t => (a -> [b]) -> t a -> [b],可以使用map和concat实现concatMap f l = let t = map f l in concat t
Prelude> null []
True
Prelude> null [1]
False
Prelude> null [[]]
False
Prelude> length [[1],[2],[]]
3
Prelude> [1,2,3,4]!!1
2
Prelude> reverse [1..10]
[10,9,8,7,6,5,4,3,2,1]
Prelude> init [1..10]
[1,2,3,4,5,6,7,8,9]
Prelude> tail [1..10]
[2,3,4,5,6,7,8,9,10]
Prelude> map (\x->x^2+1) [1..10]
[2,5,10,17,26,37,50,65,82,101]
Prelude> filter even [1..10]
[2,4,6,8,10]
Prelude> filter odd [1..10]
[1,3,5,7,9]
Prelude> filter (>6) [1..10]
[7,8,9,10]
Prelude> span even [2,4,6,7,8,9,10]
([2,4,6],[7,8,9,10])
Prelude> break even [2,4,6,7,8,9,10]
([],[2,4,6,7,8,9,10])
Prelude> takeWhile (>=5) [11,10..]
[11,10,9,8,7,6,5]
Prelude> dropWhile (>=5) [11,10,3,2,1100]
[3,2,1100]
Prelude> splitAt 5 "Hello World!"
("Hello"," World!")
Prelude> replicate 5 10
[10,10,10,10,10]
Prelude> all (>100) [1..]
False
Prelude> any (>100) [1..]
True
Prelude> elem 'l' "Helloworld"
True
Prelude> notElem 'c' "Helloworld"
True
Prelude> until (>500) (^2) 2
65536
Prelude> unzip [(1,'a'),(2,'b'),(3,'c')]
([1,2,3],"abc")
Prelude> zipWith (*) [1,3,5] [2,4,6]
[2,12,30]
Prelude> concat [[1,2,3],[4,5,6]]
[1,2,3,4,5,6]
Prelude> concatMap (replicate 3) [1,2,3]
[1,1,1,2,2,2,3,3,3]
字符串处理函数
show:可以将Show类型类的数据输出成字符串
read:类型为read :: Read a => String -> a,可以从字符串转成指定类型,可以使用::Int这样的形式来指定返回的类型,例如read "False" ::Bool
lines、unlines:lines将字符串以\n分隔在列表,而unlines是将列表以换行符组成一个字符串
words、unwords:与之前lines一致,只是使用空格分割
Prelude> map show [1..100]
["1","2","3","4","5","6","7","8","9","10"]
-- 找出1~100中有6的数字
Prelude> filter (elem '6') (map show [1..100])
["6","16","26","36","46","56","60","61","62","63","64","65","66","67","68","69","76","86","96"]
-- 将找出来的6变成Int
Prelude> map (\x->read x ::Int) $ filter (elem '6') (map show [1..100])
[6,16,26,36,46,56,60,61,62,63,64,65,66,67,68,69,76,86,96]
Prelude> lines "a\nb\n"
["a","b"]
Prelude> unlines ["a","b"]
"a\nb\n"
-- 将一句话的单词倒过来
Prelude> unwords $ reverse $ words "I am a man"
"man a am I"
字符
使用单引号的单个字母表示成字符,是其它语言中的char,Haskell中的char定义在Data.Char,可以使用:m +Data.Char来加载。
chr、ord:chr将ASCII码转成字符,ord将字符转成ASCII码
isDigit、isLower、isUpper、isAlpha、isControl:用于判断字符是否是指定类型
Prelude> :m +Data.Char
Prelude Data.Char> chr 90
'Z'
Prelude Data.Char> ord 'a'
97
Prelude Data.Char> isControl '\ESC'
True
Prelude Data.Char> isLower 'a'
True
Prelude Data.Char> isLower '\97'
True
Prelude Data.Char> isLower $ chr 97
True
位
二进制位相关的运算库位于Data.Bits中。其中定义了很多位运算相关的函数,例如5 .&. 2的值为0
(||) :: Bool -> Bool -> Bool
Prelude> :browse Data.Bits
class Eq a => Data.Bits.Bits a where
(Data.Bits..&.) :: a -> a -> a
(Data.Bits..|.) :: a -> a -> a
Data.Bits.xor :: a -> a -> a
Data.Bits.complement :: a -> a
Data.Bits.shift :: a -> Int -> a
Data.Bits.rotate :: a -> Int -> a
Data.Bits.zeroBits :: a
Data.Bits.bit :: Int -> a
Data.Bits.setBit :: a -> Int -> a
Data.Bits.clearBit :: a -> Int -> a
Data.Bits.complementBit :: a -> Int -> a
Data.Bits.testBit :: a -> Int -> Bool
Data.Bits.bitSizeMaybe :: a -> Maybe Int
Data.Bits.bitSize :: a -> Int
Data.Bits.isSigned :: a -> Bool
Data.Bits.shiftL :: a -> Int -> a
Data.Bits.unsafeShiftL :: a -> Int -> a
Data.Bits.shiftR :: a -> Int -> a
Data.Bits.unsafeShiftR :: a -> Int -> a
Data.Bits.rotateL :: a -> Int -> a
Data.Bits.rotateR :: a -> Int -> a
Data.Bits.popCount :: a -> Int
{-# MINIMAL (.&.), (.|.), xor, complement,
(shift | shiftL, shiftR), (rotate | rotateL, rotateR), bitSize,
bitSizeMaybe, isSigned, testBit, bit, popCount #-}
class Data.Bits.Bits b => Data.Bits.FiniteBits b where
Data.Bits.finiteBitSize :: b -> Int
Data.Bits.countLeadingZeros :: b -> Int
Data.Bits.countTrailingZeros :: b -> Int
{-# MINIMAL finiteBitSize #-}
Data.Bits.bitDefault :: (Data.Bits.Bits a, Num a) => Int -> a
Data.Bits.popCountDefault :: (Data.Bits.Bits a, Num a) => a -> Int
Data.Bits.testBitDefault ::
(Data.Bits.Bits a, Num a) => a -> Int -> Bool
Data.Bits.toIntegralSized ::
(Integral a, Integral b, Data.Bits.Bits a, Data.Bits.Bits b) =>
a -> Maybe b
递归函数
本节中说明递归函数,主要是以例子为主,所以列出了书中例子的实现,有一些跟书中实现一致,有一些是笔者自己编写
麦卡锡91函数的说明
\[M(n) = \begin{cases} n-10, & {(n>100)} \\ M(M(n+11)), & {(n \le 100)} \end{cases}\]等价于
\[M(n) = \begin{cases} n-10, & {(n>100)} \\ 91, & {(n \le 100)} \end{cases}\]{-# LANGUAGE BangPatterns #-}
import Prelude hiding (gcd, product)
-- 阶乘
factorial :: Integer -> Integer
factorial n | n <= 0 = error "invalid n"
| n == 1 = 1
| otherwise = n * factorial (n-1)
-- 最大公约数
gcd :: Int -> Int -> Int
gcd a b | a `mod` b == 0 = b
| otherwise = gcd b (a `mod` b)
-- 乘方
power :: Integer -> Integer -> Integer
power x n | n == 0 = 1
| otherwise = x * power x (n-1)
-- 改进乘方
power1 :: Integer -> Integer -> Integer
power1 x n | n <= 1 = x
| even n = let p = power1 x (n `div` 2) in p * p
| otherwise = let p = power1 x (n `div` 2) in x * p * p
-- 列表求积
product :: Num a => [a] -> a
product [] = 1
product (x:xs) = x * product xs
-- 将元素添加到列表的末尾(与cons即(:)运算符相反)
snoc :: a -> [a] -> [a]
snoc x [] = [x]
snoc x (y:ys) = y:(snoc x ys)
-- 删除列表中的指定的元素
delete :: Eq a => a -> [a] -> [a]
delete x [] = [];
delete x (y:ys) = if x == y then delete x ys else y : delete x ys
-- 求列表的和
total :: Num a => [a] -> a
total [] = 0
total (x:xs) = x + total xs
-- 使用尾递归求列表的和(尾递归是指递归函数return的语句只有递归函数调用本身,而没有其它运算)。将和做为参数传给函数
total1 :: Num a => [a] -> a -> a
total1 [] a = a
total1 (x:xs) a = total1 xs (x+a)
-- 由于Haskell惰性求值的特性,之前的尾递归并不能省略相应的空间,因为x+a并不是作为结果使用,在程序中也没有进行匹配判断等,所以只有在需要的时候才求值(即最后),中间的值都会暂存于内存中
-- 需要使用!模式(bang pattern)匹配(在参数匹配前计算值)或者$!运算符(在函数调用时计算值)强制求值。
-- bang pattern需要开启才能使用,在文件开头添加{-# LANGUAGE BangPatterns #-}
-- https://downloads.haskell.org/~ghc/6.8.1/docs/html/users_guide/bang-patterns.html
-- https://ocharles.org.uk/posts/2014-12-05-bang-patterns.html
total2,total3 :: Num a => [a] -> a -> a
total2 [] a = a
total2 (x:xs) !a = total2 xs (x+a)
total3 [] a = a
total3 (x:xs) a = total3 xs $! (x+a)
-- 互调递归,即函数1调用了函数2,函数2又调用了函数1
even1,odd1 :: Int -> Bool
even1 n | n == 0 = True
| otherwise = odd1 (n-1)
odd1 n | n == 0 = False
| otherwise = even1 (n-1)
-- 麦卡锡91函数,它的性质是n<=100时,结构为定值91,大于 100时,为n-10
mc91 :: Int -> Int
mc91 n | n > 100 = n-10
| otherwise = mc91 $ mc91 (n+11)
-- 斐波那契数列
fibonacci :: (Num a, Eq a) => a -> a
fibonacci 0 = 0
fibonacci 1 = 1
fibonacci n = fibonacci(n-2) + fibonacci(n-1)
-- 生成斐波那契数列列表的方法,如果使用map fibonacci [1..100],会非常慢,因为每一次都要递归求和
-- 此函数可以直接使用列表的前两个值来计算,所以速度很快
fibs :: Int -> [Integer]
fibs 1 = [1]
fibs 2 = [1,1]
fibs n = let a = fibs (n - 1) in a ++ [sum (drop (n-3) a)]
-- fastFibs,可以快速求得某个位置的数值
fibStep :: (Integer, Integer) -> (Integer,Integer)
fibStep (u,v) = (v, u+v)
fibPair :: Int -> (Integer, Integer)
fibPair 1 = (1, 1)
fibPair n = fibStep $ fibPair (n-1)
fastFib :: Int -> Integer
fastFib n = fst $ fibPair n
-- 斐波那契数列的两个性质验证
-- 前后两项的比值接近黄金分割(sqrt 5 - 1) / 2;其实以下函数是计算列表中的前后两项值的比例
-- neighborRatio $ map fromIntegral (fibs 200)
neighborRatio :: Fractional a => [a] -> [a]
neighborRatio [n] = [0]
neighborRatio [x,y] = [0, x / y]
neighborRatio xs = let p = init xs in neighborRatio p ++ [ last p / last xs]
-- 连续三项中,中间项的平方与前后项的乘积相差1
lx :: [Integer] -> [Integer]
lx [x] = []
lx [x,y] = []
lx [x,y,z] = [x*z - y^2]
lx (x:y:z:xs) = (x*z - y ^ 2) : lx (y : z : xs)
-- 10进制转罗马数字
-- 找出第一个不大于n的罗马数字,然后减掉,再计算,如此往复
romeNotation :: [String]
romeNotation = ["M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"];
romeAmount :: [Int]
romeAmount = [1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1]
conv2Rome :: Int -> String
conv2Rome 0 = ""
conv2Rome n = let combine = zip romeAmount romeNotation in
let (x, y) = head (dropWhile (\(x,y) -> x > n ) combine) in
y ++ conv2Rome(n-x)
-- 二分查找
binarySearch :: (Ord a) => a -> [a] -> Bool
binarySearch a [] = False
binarySearch a xs = let (left,mid:right) = splitAt (length xs `div` 2) xs in
a == mid ||
if a > mid then binarySearch a right
else binarySearch a left
-- 二分查找的另外一种写法
binarySearch1 :: (Ord a) => a -> [a] -> Bool
binarySearch1 a [] = False
binarySearch1 a xs | a > mid = binarySearch1 a right
| a < mid = binarySearch1 a left
| otherwise = True
where (left,mid:right) = splitAt (length xs `div` 2) xs
-- 汉诺塔(Tower of Hanoi)问题
-- (移动数量,来自哪,移到哪,借助哪) -> 操作列表
-- 使用:hanoi(10, 1, 2, 3)
hanoi :: (Int,Int,Int,Int) -> [(Int, Int)]
hanoi (1, from, to, v) = [(from, to)]
hanoi (n, from, to, v) = hanoi (n-1, from, v, to) ++ [(from, to)] ++ hanoi (n-1, v, to, from)
-- 插入排序,即往有序的列表中插入元素来达到排序的目的
-- 时间复杂度为O(n^2),虽然可以用折半查找插入来减少比较次数,但最差复杂度仍然为O(n^2),因为移动次数无法减少
insertSort :: Ord a => [a] -> [a]
-- 需要一个辅助函数,将元素插入已经排序好的列表中
insertSortInsert :: Ord a => a -> [a] -> [a]
insertSortInsert a [] = [a]
insertSortInsert a (x:xs) | a > x = x : insertSortInsert a xs
| otherwise = a:x:xs
-- 可简化成insertSort = foldr insertSortInsert
insertSort [] = []
insertSort (x:xs) = insertSortInsert x (insertSort xs)
-- 另外一种写法
insertSort1 :: Ord a => [a] -> [a] -> [a]
insertSort1 xs [] = xs
insertSort1 xs (y:ys) = insertSort1 (insertSortInsert y xs) ys
-- 冒泡排序
-- 时间复杂度为O(n^2)
bubbleSort :: Ord a => [a] -> [a]
-- 辅助函数,一趟冒泡
bubbleSortOne :: Ord a => [a] -> [a]
bubbleSortOne [] = []
bubbleSortOne [a] = [a]
bubbleSortOne (x:y:xs) | x > y = y : bubbleSortOne (x:xs)
| otherwise = x : bubbleSortOne (y:xs)
bubbleSort [] = []
bubbleSort xs = let p = bubbleSortOne xs in
bubbleSort (init p) ++ [last p]
-- 另外一种使用不动点的方式,即一直调用bubbleSortOne,直到整个列表没有变化
-- 这种做法的效率没有前面那个方法高
bubbleSort1 :: Ord a => [a] -> [a]
bubbleSort1 xs = if xs == xs' then xs else bubbleSort1 xs'
where xs' = bubbleSortOne xs
-- 选择排序,即每一次遍历取出最小的一个放在开头
selectionSort :: Ord a => [a] -> [a]
-- 辅助函数,从列表中取出最小的值,并删除这个元素
selectionSortMin :: Ord a => [a] -> (a, [a])
selectionSortMin [a] = (a, [])
selectionSortMin (x:y:xs) | x > y = let (min, dest) = selectionSortMin(y:xs) in (min, x:dest)
| otherwise = let (min, dest) = selectionSortMin(x:xs) in (min, y:dest)
selectionSort [] = []
selectionSort xs = let (min, dest) = selectionSortMin xs in min:selectionSort dest
-- 快速排序,即选取一个数,以此为分割,分成小于此数的列表和大于此数的列表,再对这两个列表进行快速排序,最后合并
-- 时间复杂度是O(nlogn)
quitSort :: Ord a => [a] -> [a]
-- 辅助函数,从列表中取出大于等于a和小于a的数
quitSortSplit :: Ord a => a -> [a] -> ([a], [a])
quitSortSplit a [] = ([], [])
quitSortSplit a (x:xs) | x >= a = (min, x:max)
| otherwise = (x:min, max)
where (min, max) = quitSortSplit a xs
quitSort [] = []
quitSort (x:xs) = let (min, max) = quitSortSplit x xs in quitSort min ++ [x] ++ quitSort max
-- 另外一种写法直接使用filter函数,但是效率上比不上前一个
quitSort1 :: Ord a => [a] -> [a]
quitSort1 [] = []
quitSort1 (x:xs) = quitSort1 min ++ [x] ++ quitSort1 max
where min = filter (<x) xs;max = filter (>=x) xs
-- 归并排序,即将两个已经排好序的列表合并成一个有序的列表
mergeSort :: Ord a => [a] -> [a]
-- 辅助函数,将两个有序的列表合并成一个
mergeSortList ::Ord a => [a] -> [a] -> [a]
mergeSortList [] a = a
mergeSortList a [] = a
mergeSortList (x:xs) (y:ys) | x > y = y : mergeSortList (x:xs) ys
| otherwise = x : mergeSortList xs (y:ys)
mergeSort [] = []
mergeSort [a] = [a]
mergeSort xs = let (left,right) = splitAt (length xs `div` 2) xs in
mergeSortList (mergeSort left) (mergeSort right)
不动点函数
匿名函数是λ表达式的广泛应用,如何在匿名函数中实现递归调用呢,那么就需要定义一个辅助fix,其定义如下
fix :: (a->a) -> a
fix f = f (fix f)
fix函数接收一个a->a类型的函数,并且不断调用f函数,例如当f参数为(1:)时,展开为:
fix (1:) = 1: (fix (1:))
= 1: 1: fix (1:)
= 1: 1: 1: fix (1:)
...
所以fix (1:)得到了一个元素为1的无穷列表,不过借助于惰性求值,使用take 10 ( fix (1:))还是可以马上得出10个1的列表,因为Haskell只在需要的时候计算值。
有了fix函数,阶乘函数就可以改写成如下方式:
factorial1 :: Integer -> Integer
factorial1 = fix (\f n -> if n == 0 then 1 else n * f (n-1))
我们将factorial1 2这个求值过程展开:
factorial1 2 = fix (\f n -> if n == 0 then 1 else n * f (n-1))
= (\f n -> if n == 0 then 1 else n * f (n-1)) ( fix (\f n -> if n == 0 then 1 else n * f (n-1)) ) 2
= 2 * ( fix (\f n -> if n == 0 then 1 else n * f (n-1)) 1 )
= 2 * ( (\f n -> if n == 0 then 1 else n * f (n-1)) (fix (\f n -> if n == 0 then 1 else n * f (n-1) )) 1 )
= 2 * 1 * ( (fix (\f n -> if n == 0 then 1 else n * f (n-1) )) 0 )
= 2 * 1 * 1
= 2
由上式可见fix函数并不是会一直无限递归下去,而是利用惰性求值的特定,在某一时刻收敛到某一个值,而返回结果。
牛顿法开方
假设 \(c = x ^2\),那么\(x = \frac c x\),此时 \(x+\frac c x = 2x\) 即 \(x = \frac { \frac c x + x} {2.0}\);可以使用此式子给定一个x初始值,不断迭代后x将逐渐趋于结果(关于这个式子为何会收敛,更严谨的证明可以查看这篇文章或者维基百科)。
-- 牛顿法开方
newton :: (Ord a,Fractional a) => a -> a
-- 辅助方法,需要给一个初始值
newtonHelper :: (Ord a,Fractional a) => a -> a -> a
newtonHelper c t = if abs (t' - t) < 1.0e-13 then t' else newtonHelper c t' where t' = (c/t + t)/2
newton c = newtonHelper c c
newtonHelper给定一个初始值,然后通过不断迭代,直到两次求得结果相差小于某个精度时,认为是结束。
*Main> sqrt 2
1.4142135623730951
*Main> newton 2
1.414213562373095
-- 有意思的是,如果给定的初始值为负数,则为负数的解
*Main> newtonHelper 2 (-100)
-1.414213562373095
*Main>
教材中使用了另外一种方法来求解,配置一个迭代次数之后递归调用:
-- 牛顿法开方递归调用解法,调用方法为newton1 2 100
newton1 :: Double -> Int -> Double
newton1 c 0 = c
newton1 c n = (c/t + t)/2 where t = newton1 c (n-1)
使用不动点的方法,目前为止还不太理解:
-- 牛顿法开方,使用不动点方式
fix1 :: (t -> t -> Bool) -> (t -> t) -> t -> t
fix1 c f x | c x (f x) = x
| otherwise = fix1 c f (f x)
newton2Helper :: Fractional a => a -> a -> a
newton2Helper c t = (c/t + t) / 2.0
newton2 :: Double -> Double
newton2 c = fix1 (\ a b -> a - b < 1.0e-13) (newton2Helper c) c
使用惰性求值的思想
如果比较两个列表哪个更长,可以使用下面这个函数:
-- 比较两个数组长度,如果第一个的长度小于等于第二个,返回True,否则返回False
shorter :: [a] -> [a] -> Bool
shorter a b | la > lb = False
| otherwise = True
where la = length a; lb = length b
但这个长度有些局限性,例如,如果某一个列表为无限列表,则就无法返回结果,另外length返回的是Int,很可能最大长度超过Int最大值,可以使用下面的方法来处理:
-- 使用惰性求值的思想
lazyShorter :: [a] -> [a] -> Bool
lazyShorter [] _ = True
lazyShorter _ [] = False
lazyShorter (x:xs) (y:ys) = lazyShorter xs ys
列表内包 (List Comprehension)
列表内包是指Haskell提供一种精简的语法来对列表中的元素进行处理。
例如以下这些例子:
-- 生成 1~10的平方
Prelude> [x^2|x<-[1..10]]
[1,4,9,16,25,36,49,64,81,100]
-- 生成1~10的平方中小于50的偶数
Prelude> [x^2|x<-[1..10], x^2 < 50, even x]
[4,16,36]
-- 还可以使用两个生成器
Prelude> [(x,y)| x<-[1..4],y<-[5..8], y-x > 3]
[(1,5),(1,6),(1,7),(1,8),(2,6),(2,7),(2,8),(3,7),(3,8),(4,8)]
map函数可以使用列表内包实现:
Prelude> map (+2) [1..10]
[3,4,5,6,7,8,9,10,11,12]
Prelude> [x+2| x <- [1..10]]
[3,4,5,6,7,8,9,10,11,12]
filter函数的列表内包实现对比:
Prelude> filter even [1..10]
[2,4,6,8,10]
Prelude> [x|x<-[1..10],even x]
[2,4,6,8,10]
使用列表内包打印乘法口诀表:
Prelude> [show x ++ "x" ++ show y ++ "=" ++ show (x*y)| x <-[1..9], y<-[1..9]]
["1x1=1","1x2=2","1x3=3","1x4=4","1x5=5","1x6=6","1x7=7","1x8=8","1x9=9","2x1=2","2x2=4","2x3=6","2x4=8","2x5=10","2x6=12","2x7=14","2x8=16","2x9=18","3x1=3","3x2=6","3x3=9","3x4=12","3x5=15","3x6=18","3x7=21","3x8=24","3x9=27","4x1=4","4x2=8","4x3=12","4x4=16","4x5=20","4x6=24","4x7=28","4x8=32","4x9=36","5x1=5","5x2=10","5x3=15","5x4=20","5x5=25","5x6=30","5x7=35","5x8=40","5x9=45","6x1=6","6x2=12","6x3=18","6x4=24","6x5=30","6x6=36","6x7=42","6x8=48","6x9=54","7x1=7","7x2=14","7x3=21","7x4=28","7x5=35","7x6=42","7x7=49","7x8=56","7x9=63","8x1=8","8x2=16","8x3=24","8x4=32","8x5=40","8x6=48","8x7=56","8x8=64","8x9=72","9x1=9","9x2=18","9x3=27","9x4=36","9x5=45","9x6=54","9x7=63","9x8=72","9x9=81"]
π的级数表示为\(4(1-\frac 1 3 + \frac 1 5 - \frac 1 7+ ...)\),这个序列可以使用列表内包来表示:
piSeries :: Int -> [Double]
piSeries n = [1 / (2 * fromIntegral k +1)* (-1)^k | k <- [0..n]]
但这个收敛太慢了,4 * (sum $ piSeries 1000000)结果为3.1415936535887745,才达到5位小数精度
我们可以使用更加快速的收敛式子:\(π = 4(\frac 1 2 - \frac 1 3 (\frac 1 2)^3 + \frac 1 5 (\frac 1 2)^5 + ...) + 4(\frac 1 3 - \frac 1 3 (\frac 1 3)^3 + \frac 1 5 (\frac 1 3)^5 + ...)\)
piSeries1 :: Int -> [Double]
piSeries1 n = [let p = 2*k+1 in 1 / fromIntegral p*(1/2)^^p * 4* (-1)^k + 1 / fromIntegral p*(1/3)^^p*4*(-1)^k | k <-[0..n]]
使用10次迭代sum $ piSeries1 10精度就已经达到7位小数了3.1415926704506854
素数问题
根据素数的定义,只能被1和本身整队的整数,我们定义判断一个数是否为素数:
-- 判断某个数是否为素数
isPrime :: Integer -> Bool
factors :: Integer -> [Integer]
factors n = [x| x <- [1..n], n `mod` x == 0]
isPrime n = factors n == [1,n]
-- 生成素数列表
primes :: Integer -> [Integer]
primes n = [x | x <- [0..n], isPrime x]
但这个判断是否素数的函数效率不怎么高,我们可以提升一些
-- 更快地判断是否是素数
isPrime' :: Integer -> Bool
isPrime' 2 = True
isPrime' n = n > 1 &&
let xs = takeWhile (\x -> x * x <= n) (2:[3,5..]) in all (\x-> mod n x /= 0) xs
结果对比:
*Main> length $ filter isPrime' [1..10000]
1229
(0.09 secs, 27,257,224 bytes)
*Main> length $ filter isPrime [1..10000]
1229
(3.14 secs, 1,161,444,288 bytes)
在密码学上经常需要给定一个大数,算出这个大数之后的第一个素数:
-- 给定一个因子,计算比它大的第一个素数
-- 这个方法还是很慢,nextPrime 24432434423421用了2秒
nextPrime :: Integer -> Integer
nextPrime n = let next = if even n then n+1 else n+2 in
if isPrime' next then next else nextPrime next
另外一种生成埃拉托斯特尼法(Eratosthenes sieve):
-- 埃拉托斯特尼法(Eratosthenes sieve)生成法,即拿前面所有的素数去测试下一个数是否为素数
-- 这个方法比之前的primes快许多
sieve :: [Integer] -> [Integer]
sieve (x:xs) = x: sieve [p | p<-xs,mod p x /= 0]
primes' = sieve [2..]
凯撒加密
凯撒加密是移位加密法,假设我们只对小写字母加密:
-- 凯撒加密
-- 假设只对小写字母加密
encode,encode' :: String -> Int -> String
shift :: Char -> Int -> Char
shift x n = chr ((ord x - ord 'a' + n) `mod` 26 + ord 'a')
encode xs n = [shift x n | x <- xs]
encode' [] _ = []
encode' (x:xs) n | isLower x = shift x n : encode' xs n
| otherwise = x : encode' xs n
decode,decode' :: String -> Int -> String
unshift :: Char -> Int -> Char
unshift x n = chr ((ord x - ord 'a' - n) `mod` 26 + ord 'a')
decode xs n = [unshift x n | x <-xs]
decode' [] _ = []
decode' (x:xs) n | isLower x = unshift x n : decode xs n
| otherwise = x : decode xs n
从这里可以看出遍历列表,对每一个元素做映射或者过滤的时候,列表内包的语法提供了很大的方便。
做计算机自动解密时,可以根据英文字母出现的频率来猜测移位的数字,即n的值。
假设一段文字每一个字母出现的概率为os,另一段出现的字母出现的概率为es,那么这两段字母出现的相同程序算法为:
\[\sum_{i=o}^{n-1} {\frac {(os_i -es_i)^2} {es_i}}\]在haskell中表示为:
-- 两组字母的相同程度
similarity :: [Float] -> [Float] -> Float
similarity xs ys = sum [(x-y) ^^ 2 / x| (x,y)<-zip xs ys]
如何计算一个字符串中各个字母出现的概率呢:
-- 统计26个小写字母出现的次数
stat :: String -> [Int]
stat xs = let letters = ['a'..'z'] in [length [y|y<-xs, y==x] | x<-letters]
-- 计算es
es :: [Int] -> [Float]
es xs = let n = sum xs in [fromIntegral x / fromIntegral n * 100 | x <- xs ]
已知正常的字母出现的概率为:
-- 正常字母出现的百分比为
os :: [Float]
os = [8.2,1.5,2.8,4.3,12.7,2.2,2.0,6.1,7.0,0.2,0.8,4.0,2.4,6.7,7.5,1.9,0.1,6.0,6.3,9.1,2.8,1.0,2.4,0.2,2.0,0.1]
则可以通过以下式子找出最合理的猜测:
-- 猜测
guess :: String -> String
-- 取出最相似的一组,即值最小
guessFindMin :: [(Float, String)] -> String
guessFindMin [(x, y)] = y
guessFindMin ((x1,y1):(x2,y2):xs) | x1 > x2 = guessFindMin ((x2,y2):xs)
| otherwise = guessFindMin ((x1,y1):xs)
guess secret = guessFindMin m
where posibles = [decode secret x | x <- [0..25]]
rates = [es $ stat xs|xs <- posibles]
similaritys = [ similarity os xs|xs<-rates]
m = zip similaritys posibles
-- 展示所有结果的概率
guess' secret = m
where posibles = [decode secret x | x <- [0..25]]
rates = [es $ stat xs|xs <- posibles]
similaritys = [ similarity os xs|xs<-rates]
m = zip similaritys posibles
我们进行演试一下:
-- 加密一句话
*Main> encode "God created You, in the image and likeness of God. You have created the rest." 5
"Gti hwjfyji Ytz, ns ymj nrflj fsi qnpjsjxx tk Gti. Ytz mfaj hwjfyji ymj wjxy."
-- 使用猜测函数正确猜出了对应的值
*Main> guess "Gti hwjfyji Ytz, ns ymj nrflj fsi qnpjsjxx tk Gti. Ytz mfaj hwjfyji ymj wjxy."
"God created You, in the image and likeness of God. You have created the rest."
-- 可以看一下概率的相似度,正确的一组为22.213945,还是领先其它组很多的
*Main> guess' "Gti hwjfyji Ytz, ns ymj nrflj fsi qnpjsjxx tk Gti. Ytz mfaj hwjfyji ymj wjxy."
[(2270.915,"Gti hwjfyji Ytz, ns ymj nrflj fsi qnpjsjxx tk Gti. Ytz mfaj hwjfyji ymj wjxy."),(549.15356,"Gsh gviexih Ysy, mr xli mqeki erh pmoiriww sj Gsh. Ysy lezi gviexih xli viwx."),(527.5882,"Grg fuhdwhg Yrx, lq wkh lpdjh dqg olnhqhvv ri Grg. Yrx kdyh fuhdwhg wkh uhvw."),(1268.1891,"Gqf etgcvgf Yqw, kp vjg kocig cpf nkmgpguu qh Gqf. Yqw jcxg etgcvgf vjg tguv."),(386.43427,"Gpe dsfbufe Ypv, jo uif jnbhf boe mjlfoftt pg Gpe. Ypv ibwf dsfbufe uif sftu."),(22.213945,"God created You, in the image and likeness of God. You have created the rest."),(1196.5046,"Gnc bqdzsdc Ynt, hm sgd hlzfd zmc khjdmdrr ne Gnc. Ynt gzud bqdzsdc sgd qdrs."),(539.582,"Gmb apcyrcb Yms, gl rfc gkyec ylb jgiclcqq md Gmb. Yms fytc apcyrcb rfc pcqr."),(1602.0659,"Gla zobxqba Ylr, fk qeb fjxdb xka ifhbkbpp lc Gla. Ylr exsb zobxqba qeb obpq."),(1220.2072,"Gkz ynawpaz Ykq, ej pda eiwca wjz hegajaoo kb Gkz. Ykq dwra ynawpaz pda naop."),(4433.246,"Gjy xmzvozy Yjp, di ocz dhvbz viy gdfziznn ja Gjy. Yjp cvqz xmzvozy ocz mzno."),(641.06085,"Gix wlyunyx Yio, ch nby cguay uhx fceyhymm iz Gix. Yio bupy wlyunyx nby lymn."),(2048.8096,"Ghw vkxtmxw Yhn, bg max bftzx tgw ebdxgxll hy Ghw. Yhn atox vkxtmxw max kxlm."),(726.1493,"Ggv ujwslwv Ygm, af lzw aesyw sfv dacwfwkk gx Ggv. Ygm zsnw ujwslwv lzw jwkl."),(942.17664,"Gfu tivrkvu Yfl, ze kyv zdrxv reu czbvevjj fw Gfu. Yfl yrmv tivrkvu kyv ivjk."),(1449.1887,"Get shuqjut Yek, yd jxu ycqwu qdt byauduii ev Get. Yek xqlu shuqjut jxu huij."),(320.61365,"Gds rgtpits Ydj, xc iwt xbpvt pcs axztcthh du Gds. Ydj wpkt rgtpits iwt gthi."),(294.86188,"Gcr qfsohsr Yci, wb hvs waous obr zwysbsgg ct Gcr. Yci vojs qfsohsr hvs fsgh."),(984.00073,"Gbq perngrq Ybh, va gur vzntr naq yvxrarff bs Gbq. Ybh unir perngrq gur erfg."),(4217.6826,"Gap odqmfqp Yag, uz ftq uymsq mzp xuwqzqee ar Gap. Yag tmhq odqmfqp ftq dqef."),(1038.5636,"Gzo ncplepo Yzf, ty esp txlrp lyo wtvpypdd zq Gzo. Yzf slgp ncplepo esp cpde."),(350.89883,"Gyn mbokdon Yye, sx dro swkqo kxn vsuoxocc yp Gyn. Yye rkfo mbokdon dro bocd."),(1156.3209,"Gxm lanjcnm Yxd, rw cqn rvjpn jwm urtnwnbb xo Gxm. Yxd qjen lanjcnm cqn anbc."),(824.16907,"Gwl kzmibml Ywc, qv bpm quiom ivl tqsmvmaa wn Gwl. Ywc pidm kzmibml bpm zmab."),(606.0503,"Gvk jylhalk Yvb, pu aol pthnl huk sprlulzz vm Gvk. Yvb ohcl jylhalk aol ylza."),(1856.387,"Guj ixkgzkj Yua, ot znk osgmk gtj roqktkyy ul Guj. Yua ngbk ixkgzkj znk xkyz.")]
排列问题
全排列问题的解决办法是依次将队列中的每一个元素放在最前面,然后递归求剩下列表的全排列,最后再将结果合并:
-- 全排列问题
-- 思路:将列表中的每一个元素今次取出做为第一个,计算剩下数组的全排列,最后把这些全排列合并
permutationWithPre :: Eq a => [a] -> [a] ->[[a]]
permutationWithPre pre [] = [pre]
permutationWithPre pre ys = concat [permutationWithPre (pre ++ [a]) ax |(a:ax) <- tmp]
where tmp = [x : delete x ys|x <- ys]
permutation :: Eq a => [a] -> [[a]]
permutation = permutationWithPre []
-- *Main> permutationWithPre' [] "abcd"
-- ["abcd","abdc","acbd","acdb","adbc","adcb","bacd","badc","bcad","bcda","bdac","bdca","cabd","cadb","cbad","cbda","cdab","cdba","dabc","dacb","dbac","dbca","dcab","dcba"]
教材中应用这一思想更简单的方法:
permutation' :: Eq a => [a] -> [[a]]
permutation' [] = [[]]
permutation' xs = [x:ys |x <- xs, ys <- permutation' (delete x xs)]
全排列还可以使用插入法来解决,其思路为取出一个元素x,除去这个元素剩下的列表xs,则将x插入xs全排列中每一个列表的每一个位置,即可得到x:xs的全排列:
-- 插入法全排序
permutation'' :: Eq a => [a] -> [[a]]
insert :: a -> [a] -> [[a]]
insert x [] = [[x]]
insert x (y:ys) = (x:y:ys) : [ y:a|a<-insert x ys]
permutation'' [] = [[]]
permutation'' (x:xs) = concat [insert x ys |ys<- permutation'' xs]haskell
错位排列问题,即求一个1~n的列表的全排列表 ,但要排除掉第i位是i的情况。
思路与全排列一致,只是取出的数字需要判断一下对应位置是否可以放置
derangements :: [Int] -> [[Int]]
derangements [] = [[]]
derangements xs = map reverse [x:yx|x<-xs,x/=length xs,yx <- derangements (delete x xs)]
这个方法生成的列表的顺序是反的,需要重新反转一下:
*Main> map reverse $ derangements [1,2,3,4]
[[4,3,2,1],[3,4,2,1],[2,3,4,1],[4,3,1,2],[3,4,1,2],[3,1,4,2],[2,4,1,3],[4,1,2,3],[2,1,4,3]]
组合问题
获取列表的所有子集
-- 获取一个集合的所有子集
-- 思路为,对于第一个元素和剩余的列表,所有子集为第一个元素出现与剩下列表的所有子集合并、第一个元素不出现的情况,即剩下列表的所有子集
-- *Main> powset [1,2,3]
-- [[1,2,3],[2,3],[1,3],[3],[1,2],[2],[1],[]]
powset :: [a] -> [[a]]
powset [] = [[]]
powset (x:xs) = concat [[x:ys,ys] | ys <- powset xs]
从集合中取出n个元素:
-- 从集合中取出n个元素
-- 思路为,取出第一个元素,如果留下,递归取剩下列表的n-1个元素,如果不留下,取剩下列表的n个元素
conbinations :: Int -> [a] -> [[a]]
conbinations 0 _ = [[]]
conbinations _ [] = []
conbinations n (x:xs) = [x:ys|ys <- conbinations (n-1) xs] ++ conbinations n xs
-- 教材中解法
conbinations' :: Int -> [a] -> [[a]]
conbinations' 0 _ = [[]]
conbinations' n xs = [y:ys | y:xs' <- tails xs, ys <- conbinations' (n-1) xs']
八皇后问题
-- 8皇后问题
-- 用一个列表皇后的摆放位置,其中第n一个元素表示第n列,元素的值表示排放在此列的第几行,这样本身就限制了两个皇后不能摆同一列的规则
positions :: Int -> Int -> [[Int]]
positions 0 _ = [[]]
positions k n = [x:ys | x<-[1..n], ys<-positions (k-1) n]
-- 以下是限定条件
-- 1. 任意两个皇后不能在同一行
notSameRow :: [Int] -> Bool
notSameRow [] = True
notSameRow (x:xs) = notElem x xs && notSameRow xs
-- 2. 不能出现在同一对角线上
-- 不在同对角线,即行之差与列之差的绝对值不相等
notSameDiag :: [Int] -> Bool
notSameDiag [] = True
-- @符号表示第一个参数指向第二个参数,即xs指向(_:xs')
notSameDiag xs@(_:xs') = and [abs (i1-i) /= abs (p1-p)|(i,p)<-ip] && notSameDiag xs'
where (i1,p1):ip = zip [1..] xs
-- 8皇后问题用这个方法求解没有办法,因为8^8为16777216,即positions 8 8 生成的列表太大,无法在短时间内处理完成,我们可以看一下positions 4 4 的处理结果
queen :: Int -> [[Int]]
queen n = [xs| xs <- positions n n, notSameDiag xs, notSameRow xs]
-- *Main Data.List> queen 4
-- [[2,4,1,3],[3,1,4,2]]
-- 为了在有效时间内解决8皇后问题,我们优化一下positions方法,即在生成列表阶段就把两个限制条件给应用了
positions' :: Int -> Int -> [[Int]]
positions' 0 _ = [[]]
-- 检查生成的数和后面的数列是否满足要求
positions' k n = [x : ys | ys <- positions' (k - 1) n, x <- [1 .. n], safe x ys]
where safe e l = notElem e l && all (\(dist, p) -> dist /= abs (p-e)) (zip [1..] l)
-- 使用positions' 8 8即可生成,一共是92种方式,只使用了0.02秒不到
-- 但是,如果写成positions' k n = [x : ys | x <- [1 .. n], ys <- positions' (k - 1) n, safe x ys],即x先生成 再生成ys的话,就还是很慢
矩阵乘法
-- 矩阵转置
-- 思路:先取第一个列,然后去掉数组的第一列,递归求转置
transpose :: Num a => [[a]] -> [[a]]
transpose [] = []
transpose ([]:xss) = transpose xss
transpose ((x:xs):xxs) = (x:[y | (y : _) <- xxs]) : transpose (xs : [ys | (_ : ys) <- xxs])
-- 矩阵乘法
-- 定义符号|*|为矩阵乘法
(|*|) :: Num a => [[a]] -> [[a]] -> [[a]]
(|*|) [] _ = []
(|*|) (x:xs) b = [sum $ zipWith (*) x y |y <- b'] : (|*|) xs b
where b' = transpose b
斐波那契数列的计算方法也可以使用如下数组来乘法来表示
\[{\begin{bmatrix}1&1 \\ 1& 0\end{bmatrix}}^n = \begin{bmatrix}F_{n+1}&F_n \\ F_n&F_{n-1}\end{bmatrix}\]这个式子使用数学归纳法很容易证明其正确性,这样我们计算斐波那契数列就可以转成如下程序:
-- 斐波那契数列的矩阵求法
fibMatrix :: Integer -> [[Integer]]
fibMatrix 1 = [[1,1],[1,0]]
fibMatrix n | even n = let n' = n `div` 2; m = fibMatrix n' in m |*| m
| otherwise = let n' = (n-1) `div` 2 ; m = fibMatrix n' in m |*| m |*| fibMatrix 1
图的最短路径方法
如下无向图,有A,B,C,D四个地方,各边的距离如图:
A -8- B
| |
2 1
| |
C -4- D
则此图表示成矩阵为:(由于是无向图,所以矩阵是对称的,Inf表示不可达)
\[\begin{array}{c|lcr} {distance} & A & B & C & D \\ \hline A & 0 & 8 & 2 & Inf \\ B & 8 & 0 & Inf & 1 \\ C & 2 & Inf & 0 & 4 \\ D & Inf & 1 & 4 & 0 \end{array}\]如果要求走两步,求出A到D的最短路径,则需要计算出A->A->D,A->B->D,A->C->D,A->D->D这4条路径,然后取出距离最小的为A->D的最优值。
如果走三步,其结果为走两步到各点最优的值,再加上前两步目的地到终点最优的值,这些值中取最小的。
整理可知 \(m_{ij}^{n+1} = minimum(m_{ik}^n+m_{kj}^1)(k=1..p)\) ,可以看出这是一个不断迭代的过程。
如之前的矩阵,进行一次迭代时,A到D的最短路径为矩阵的A行和D列各元素相加取最小的,以此类推,很容易求出全矩阵的迭代n次最优解。
实现如下:
-- 图的最短路径
-- 定义一些基本结构,,Name表示地点名称,Direction表示
type Distance = Double -- 表示距离
type Name = String -- 地点名称
type Direction = String --路径描述,如A->B->C
type Weight = (Distance, Direction) -- 距离与路径描述的二元组
type RouteMap = [[Weight]] -- 描述路径距离的矩阵
-- 将名字映射成矩阵,例如zipD ["A", "B", "C", "D"] => [["A->A","A->B","A->C","A->D"],["B->A","B->B","B->C","B->D"],["C->A","C->B","C->C","C->D"],["D->A","D->B","D->C","D->D"]]
zipD :: [Name] -> [[String]]
zipD ns = [[a ++ "->" ++ b|b <- ns ] | a <- ns]
-- 将距离数组和名字映射成的矩阵,合并
zipW :: [[Distance]] -> [Name] -> RouteMap
zipW ds ns = [zip d n | (d,n)<-zip ds $ zipD ns]
-- 两个距离相连接,注意第一个Weight的目的地和第二个的出发地要一样,例如tuplePlus (1.0, "A->B->C") (2.0, "C->D->F") => (3.0,"A->B->C->D->F")
tuplePlus :: Weight -> Weight -> Weight
tuplePlus (d1, n1) (d2, n2) = (d1+d2, n1++left)
where (_, left) = break (=='-') n2
-- 进行一次迭代,取出这次迭代中距离最小的
step :: RouteMap->RouteMap->RouteMap
step a b = [[minimumBy (comparing fst) $ zipWith tuplePlus ar bc | bc<-transpose b]|ar<-a]
-- 进行n次迭代的函数
iteration :: Int -> (a->a)->a->a
iteration 0 _ x = x
iteration n f x = iteration (n-1) f (f x)
-- 定义走n步的最优解
steps :: Int -> RouteMap ->RouteMap
steps n route = iteration n (step route) route
-- 不动点函数,即矩阵中的距离不再变化
fix f x = if dss == dss' then x else fix f x'
where x' = f x
dss = [map fst ds | ds <- x']
dss' = [map fst ds | ds <- x]
-- 最终的求最优解的函数
path :: [[Distance]] -> [Name] -> RouteMap
path dis ns = fix (step route) route
where route = zipW dis ns
-- i表示无穷远,即不连通
i = 1/0
-- 以下是例子,定义了一个无向图
graph = [[0,1,i,i,i,i,i,1,i,i],
[1,0,1,i,i,i,i,i,i,i],
[i,1,0,i,i,i,i,i,1,1],
[i,i,i,0,1,1,i,i,i,i],
[i,i,i,1,0,i,i,i,i,i],
[i,i,i,1,i,0,i,i,1,i],
[i,i,i,i,i,i,0,i,1,i],
[1,i,i,i,i,i,i,0,i,i],
[i,i,1,i,i,1,1,i,0,i],
[i,i,1,i,i,i,i,i,i,0]]
-- 地点名称
names = ["A","B","C","D","E","F","G","H","I","J"]
-- 例子 path graph names
使用此方法,计算开头的例子结果如下:
*Main> path [[0,8,2,i],[8,0,i,1],[2,i,0,4],[i,1,4,0]] ["A","B","C","D"]
[[(0.0,"A->A->A->A"),(7.0,"A->C->D->B"),(2.0,"A->A->A->C"),(6.0,"A->A->C->D")],[(7.0,"B->D->C->A"),(0.0,"B->B->B->B"),(5.0,"B->B->D->C"),(1.0,"B->B->B->D")],[(2.0,"C->A->A->A"),(5.0,"C->C->D->B"),(0.0,"C->C->C->C")
,(4.0,"C->C->C->D")],[(6.0,"D->C->A->A"),(1.0,"D->B->B->B"),(4.0,"D->C->C->C"),(0.0,"D->D->D->D")]]
所以A->B的最优解为A->C->D->B,花费为7。
高阶函数与复合函数
高阶函数是指参数为函数或者返回函数的函数,例如 map,span,还有我们之前的不动点函数等等。
这里着重介绍foldr和foldl两个函数。
我们很熟悉sum,product这些对列表求和或求积的函数,他们的定义如下形式
product [] = 1
product (x:xs) = x * product xs
sum [] = 0
sum (x:xs) = x + sum xs
and [] = True
and (x:xs) = x && and xs
更一般的,这种形式的列表函数可以表示为
f [] = e
f (x:xs) = x ⊙ f xs
其中e称之为x类型的单位元,如加法单位元是0,乘法为1。
像这种形式的列表操作函数,可以使用foldl(向左折叠),foldr(向右折叠)来定义:
-- 或者η简化为 sum = foldr (+) 0
sum xs = foldr (+) 0 xs
and xs = foldr (&&) True xs
foldr是给右结合性的操作符使用的,它是个扩展递归函数,其定义为:
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)
所以如下操作的返回值:
foldr (:) [1,2,3] [4,5,6]
= (:) 4 (foldr (:) [1,2,3], [5,6])
= (:) 4 ((:) 5 (foldr (:) [1,2,3], [6]))
= (:) 4 ((:) 5 ((:) 6 (foldr (:) [1,2,3], []])))
= (:) 4 ((:) 5 ((:) 6 [1,2,3])
= [4,5,6,1,2,3]
还有一些其它的例子:
import Prelude hiding (concat,map)
-- 使用foldr定义函数
-- ++操作符相反的操作符
-- [1,2,3] +++ [4,5,6] => [4,5,6,1,2,3]
(+++) :: [a] -> [a] -> [a]
(+++) = foldr (:)
-- 插入排序使用foldr的写法
-- isSort [1,5,2,10,8,0,9] => [0,1,2,5,8,9,10]
insert :: Ord a => a -> [a] -> [a]
insert x [] = [x]
insert x (y:ys) | x < y = x:y:ys
| otherwise = y:insert x ys
isSort :: Ord a => [a] -> [a]
isSort = foldr insert []
-- 将列表中连续相同的元素去重只保留一个
-- compress [1,2,3,3,4,5,6,6,6,6,6,6,6,6,9,6,4,9,9,9,9,9] => [1,2,3,4,5,6,9,6,4,9]
skip :: Eq a => a -> [a] -> [a]
skip x [] = [x]
skip x (y:ys) | x == y = y:ys
| otherwise = x:y:ys
compress :: Eq a => [a] -> [a]
compress = foldr skip []
-- 将元素追加到列表尾部
-- snoc 1 [2,3,4]=>[2,3,4,1]
snoc :: a -> [a] -> [a]
snoc x = foldr (:) [x]
-- 连接操作符
-- concat [[1,2,3],[4,5,6]] => [1,2,3,4,5,6]
concat :: [[a]] -> [a]
concat = foldr (++) []
-- map的另外一个实现
-- map (+1) [1,2,3] = [2,3,4]
map :: (a->b) -> [a] -> [b]
map f = foldr (\x y->f x : y) []
与foldr相反的函数foldl要求操作符需要是左结合性的。foldl是尾递归,但由于惰性求值的存在,foldl还是会存储中间值,可以使用非惰性求值的版本foldl’来强制表达式求值。
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs
看如下的例子:
-- 翻转列表
-- reverse [1,2,3] => [3,2,1]
reverse :: [a] -> [a]
reverse = foldl (flip (:)) []
还有一些函���如foldr1和foldl1(以及与之对应的foldl1’(Data.List库中)这些函数,他们的定义分别如下:
foldl1 :: (a -> a -> a) -> [a] -> a
foldl1 f (x:xs) = foldl f x xs
foldl1 _ [] = error "Prelude.foldl1: empty list"
foldr1 :: (a -> a -> a) -> [a] -> a
foldr1 f [x] = x
foldr1 f (x:xs) = f x (foldr1 f xs)
foldr1 _ [] = error "Prelude.foldr1: empty list"
-- 将字符串列表用空格连接起来
unwords :: [String] -> String
unwords [] = ""
-- 这里其实使用foldr1也是一样的
unwords xs = foldl1 (\s sl-> s++" "++sl) xs
两个可以记录中间状态的函数mapAccumL和mapAccumR,其定义在Data.List中。
例如,求和运算,记录每一次求和的奇偶情况:
Prelude Data.List> mapAccumL (\sum x-> (sum +x, even $ sum+x)) 0 [1,3,5,7,9]
(25,[False,True,False,True,False])
Prelude Data.List> mapAccumR (\sum x-> (sum +x, sum+x)) 0 [1,3,5,7,9]
(25,[25,24,21,16,9])
Prelude Data.List> mapAccumL (\sum x-> (sum +x, sum+x)) 0 [1,3,5,7,9]
(25,[1,4,9,16,25])
复合函数
在数学中如果有\(f(x) = 4x+1, g(x) = x^2+1\),那么\(h(x) = f(g(x)) = 4g(x)+1 = 4(x^2+1) +1\)。
此即所谓的复合函数,即先求g(x)的值,然后将g(x)的值代入f(x)求得最终的结果。在Haskell中,使用(.)运算符来表示复合函数,其定义为:
(.) :: (b->c) ->(a->b) -> (a->c)
(.) f g = \x -> f (g x)
之前的例子表示为:
Prelude> f = \x -> 4*x+1;
Prelude> g = \x -> x^2 +1
Prelude> (f.g) 2
21
由于(.)的运算参数是从左到右,而计算过程则为从右往左,所以看(.)的类型签名显得有些怪异,可以定义(>>)运算符来调转反置复合函数参数的顺序:
-- 定义从左到右的复合函数计算运算符
infix 9 >>
(>>) :: (a->b) -> (b->c) -> (a->c)
(>>) = flip (.)
-- *Main> (g>>f) 2
-- 21
如果将参数往前提,可以定义(|>)运算符来实现:
-- 定义参数前置的复合函数运算符
(|>) :: b -> (b->c) -> c
(|>) = flip ($)
-- *Main> 2 |> g |> f
-- 21
一些库函数使用复合函数的实现:
-- 库函数使用复合函数来实现
any',all' :: (a->Bool) -> [a] -> Bool
any' p = or . map p
all' p = and . map p
elem',notElem' :: Eq a => a -> [a] -> Bool
elem' = any' . (==)
notElem' = all' . (/=)
定义数据类型
枚举类型
-- 自定义bool类型
-- data为类型定义关键字,类型名称大写,这里的MyBool是个枚举类型,只有两个值
data MyBool = MyFalse | MyTrue
-- 定义星期类型,它也是个枚举类型
-- 定义中的deriving表示这个类型自动实现导入类型类中对应的函数
-- Show,所以可以在ghic中打印出对应的值,如果没有Show将会报错
-- Eq,可比较相等
-- Ord,可比较大小
-- Enum,可以使用[Mon .. Sun]来枚举生成列表,注意这里..的之前要有空格
-- Read,可以将一个字符串读取成Day类型,例如read "Mon"::Day => Mon,read "[Mon,Tue]"::[Day] => [Mon,Tue]
data Day = Mon | Tue | Wed | Thu | Fri | Sat | Sun deriving (Show, Eq, Ord, Enum, Read)
-- 根据Day类型,定义tomorrow
tomorrow :: Day -> Day
tomorrow Mon = Tue
tomorrow Tue = Wed
tomorrow Wed = Thu
tomorrow Thu = Fri
tomorrow Fri = Sat
tomorrow Sat = Sun
tomorrow Sun = Mon
-- 由于实现了Enum类型类所以可以使用succ和pred函数
tomorrow1,yestoday :: Day -> Day
tomorrow1 Sun = Mon
tomorrow1 n = succ n
yestoday Mon = Sun
yestoday n = pred n
构造类型
-- 构造类型,有点类似于C语言中的Struct,需要多个其它类型的数据来构建这个类型的数据
type Name = String
type Author = String
type ISBN = String
type Price = Float
-- 如下定义了Book类型,这个Book即是类型,也是函数,称为数据构造器,其名字并非只能与类型名一致
-- 所以这个定义也可以data Book = BookCon Name Author ISBN Price deriving (Show, Eq)
data Book = Book Name Author ISBN Price deriving (Show, Eq)
-- 属性的访问器
name :: Book -> Name
name (Book n _ _ _) = n
author :: Book -> Author
author (Book _ a _ _) = a
isbn :: Book -> ISBN
isbn (Book _ _ i _) = i
price :: Book -> Price
price (Book _ _ _ p) = p
-- 但这种属性访问器写起来繁琐,另外一种更简单的方式如下:
-- 这种写法与之前的写法等价
data Book' = Book' {
name' :: Name,
author' :: Author,
isbn' :: ISBN,
price' :: Price
}
对于以上的定义,Book即是类型,也是函数,被称为数据构造器:
*Main> :t Book
Book :: Name -> Author -> ISBN -> Price -> Book
*Main> :k Book
Book :: *
-- 简单的使用
*Main> let t = Book "name" "author" "2424234" 1.1
*Main> :t t
t :: Book
*Main> name t
"name"
*Main> price t
1.1
-- Book'的定义是等价的
*Main> let t = Book' "book" "author" "isb" 2.2
*Main> :t t
t :: Book'
*Main> name' t
"book"
*Main> isbn' t
"isb"
以Book为基础 ,定义涨价函数,这个函数会把原价格和涨价后的价格都记录成列表:
-- 涨价
incrisePrice :: ([Book], [Book]) -> Book -> Float -> ([Book],[Book])
incrisePrice (b1,b2) b pri = (b : b1, Book (name b) (author b) (isbn b) (price b + pri) : b2)
-- 可以使用@符号来减少冗长的表达式(其实都一样)
incrisePrice' :: ([Book], [Book]) -> Book -> Float -> ([Book],[Book])
incrisePrice' (b1,b2) b@(Book nm ath isn prc) pri = (b : b1, Book nm ath isn (prc + pri) : b2)
例子
*Main> let t = Book "book" "author" "isb" 2.2
*Main> incrisePrice ([],[]) t 1
([Book "book" "author" "isb" 2.2],[Book "book" "author" "isb" 3.2])
Book的构造器需要其它参数来填充,而像True或者False这些布尔构造器并不需要参数,这种称之为零元数据构造器(nullary data constructor)。
参数化类型
即需要一个类型参数来构造的类型,例如标准库中的Maybe,其实定义为:
data Maybe a = Nothing | Just a deriving (Eq, Ord, Read, Show)
Maybe类型的主要作用是进行简单的程序异常处理,例如head函数在列表为空的时候会抛出异常,我们可以定义一个返回Maybe类型的safeHead,在为空时返回Nothing:
-- 空列表安全的head
safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:_) = Just x
像Maybe这种以类型做为构造器参数的称之为类型构造器,可以使用:kind命令查看某一个类型所需要的类型参数,*表示不需要其它类型,称之为零元类型构造器,其它需要参数的使用箭头来表示需要的类型个数,例如:
*Main> :k Int
Int :: *
*Main> :k Book
Book :: *
*Main> :k Maybe
Maybe :: * -> *
*Main> :k Either
Either :: * -> * -> *
我们来看看Either的定义:
data Either a b = Left a | Right b deriving (Eq, Ord, Read, Show)
正常列表中的值必须一样,但使用Either就可以保存两种不一样的类型了,例如对于学生成绩列表,有些同学没有成绩,这时需要保存没有成绩的理由,那么就可以使用如下形式:
*Main> let t = [Left 80, Right "Cheated", Left 100, Left 60, Right "Cheated"]
*Main> :t t
t :: Num a => [Either a [Char]]
将两个类型不同的列表合并成一个Either类型的列表函数:
-- 合并两个类型不一样的列表为一个列表
disjoint :: [a] -> [b] -> [Either a b]
disjoint as bs = [Left a | a <- as] ++ [Right b| b <- bs]
-- disjoint [1,2,3,4] "abcdefg" => [Left 1,Left 2,Left 3,Left 4,Right 'a',Right 'b',Right 'c',Right 'd',Right 'e',Right 'f',Right 'g']
-- disjoint 反函数
partitionEithers :: [Either a b] -> ([a], [b])
partitionEithers [] = ([],[])
partitionEithers (Left x : xs) = (x:l, r) where (l,r) = partitionEithers xs
partitionEithers (Right x : xs) = (l, x:r) where (l,r) = partitionEithers xs
-- partitionEithers [Left 1,Left 2,Left 3,Left 4,Right 'a',Right 'b',Right 'c',Right 'd',Right 'e',Right 'f',Right 'g'] => ([1,2,3,4],"abcdefg")
参数化类型声明时还可以对类型参数进行限定,例如:
-- 将Shape接受的类型参数限定在Num类型
-- 这时必须加上{-# LANGUAGE DatatypeContexts #-},但是这个已经被淘汰了,所以不推荐使用,推荐使用GADTs来代替
data (Num a) => Shape a = Rectangular a a
下面来看看一下二元元组构造器(,),和三元元组构造器(,,)
*Main> let t = (,) 1 2
*Main> :t t
t :: (Num a, Num b) => (a, b)
*Main> :k t
<interactive>:1:1: error: Not in scope: type variable ‘t’
*Main> :i t
t :: (Num a, Num b) => (a, b) -- Defined at <interactive>:56:5
*Main> let t2 = (,,) 1 'a' 3
*Main> t2
(1,'a',3)
*Main> :t t2
t2 :: (Num a, Num c) => (a, Char, c)
函数本身也是一种类型,其构造器为(->),其king为 ->->*。
递归类型
首先定义一种基本情况,然后在定义中又用到了此数据类型,这种定义类型被称之为递归类型。
-- 递归定义自然数
data Nat = Zero | Succ Nat deriving (Show, Eq, Ord)
-- int转自然数
-- int2nat 10 => Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Succ Zero)))))))))
int2nat :: Int -> Nat
int2nat 0 = Zero
int2nat n = Succ $ int2nat $ n-1
-- 自然数转Int
-- nat2int $ Succ $ int2nat 10 => 11
nat2int :: Nat -> Int
nat2int Zero = 0
nat2int (Succ n) = nat2int n + 1
-- 自然数的运算
add :: Nat -> Nat -> Nat
add Zero b = b
add (Succ a) b = Succ (add a b)
-- *Main> nat2int $ add (int2nat 10) (int2nat 10) => 20
混合多种方式定义类型
在实际应用中,一般都是通过结合多种之前说过的定义类型方式来定义新类型。
-- 结合枚举和构造方式定义的类型
-- 定义形状类型,包括圆和长方形
data Shape = Circle{
radius::Float
}|Rect{
width::Float,
height::Float
}
-- 定义面积函数
area :: Shape -> Float
area (Rect a b) = a * b
area (Circle r) = pi * r * r
-- 结合枚举和递归方式定义的类型
-- 定义布尔语言
data BoolExp = TRUE | FALSE | IF BoolExp BoolExp BoolExp
-- 计算值
eval :: BoolExp -> Bool
eval TRUE = True
eval FALSE = False
eval (IF a b c) = if eval a then eval b else eval c
-- eval $ IF TRUE FALSE TRUE => False
-- 参数化递归类型
-- 列表的定义,原生列表的定义为 data [] a = [] | a : [a]
-- 定义一个与原生类型等价的列表
data List a = Nil | Cons a (List a) deriving (Show, Eq)
lhead :: List a -> a
lhead Nil = error "nil list"
lhead (Cons x _) = x
-- 与标准列表的转化
list2myList [] = Nil
list2myList (x:xs) = Cons x (list2myList xs)
myList2list Nil = []
myList2list (Cons x xs) = x:myList2list xs
类型的同构
之前定义的List类型与标准库中的列表类型是等价的,可以互相转化,这种等价告之为同构(isomorphism)。
以下利用枚举定义的类型也是属于同构,因为可以定义两个转化函数来一一对应:
-- 同构类型
data ThreeNum = One | Two | Three
data Level = Low | Middle | High
f :: ThreeNum -> Level
f One = Low
f Two = Middle
f Three = High
g :: Level -> ThreeNum
g Low = One
g Middle = Two
g High = Three
若一个类型的值有无穷多个,则需要了解基数(cardinal number)的概念来区别不同的等级的无穷才能更一般地判断两个类型是否同构。
另外一个重要点就是模式匹配必须是构造器,例如我们可以使用f (x:xs) = x,但我们不能使用f ([x] ++ xs) = x,因为++不是列表构造器,不能出现在模式匹配中。
@todo 这块作者还讲了关于值个数的理论,后续有需要补充。
newtype构造器
newtype只支持单一构造器,也就是说newtype不能定义枚举类型,在这一点上,完全可以使用data来代替。
newtype与别名关键字type有点类似,但newtype会创建新类型,一般newtype用整合多个类型,例如:
newtype T a b = NewType (a,b)
newtype不同于data的地方在于data定义的类型会在编译系统类型检查和运行中产生额外的计算,因为需要构造数据而加一层包装。而newtype因为只有一个构造器且构造器只有一个参数,所以不需要额外计算。
另外newtype不同于type正如之前所说newtype定义出一种新的类型,可以在类型上实现某个类型类,例如如下的例子:
-- 使用newtype定义的类型实现Show类型类
-- Second 1 => 1 sencod
newtype Second = Second Int
instance Show Second where
show (Second 0) = "0 secnod"
show (Second 1) = "1 secnod"
show (Second n) = show n ++ " secnods"
树
树的一些定义方式:
-- 树的定义
-- 节点和叶子都可以存储内容的树
data Tree a = Leaf a | Node a (Tree a) (Tree a)
-- 只有叶子节点可以存数据的树
data Tree1 a = Leaf1 a | Node1 (Tree1 a) (Tree1 a)
-- 只有节点存储数据的树
data Tree2 a = Leaf2 |Node2 a(Tree2 a) (Tree2 a)
-- 多叉树
data Tree3 a = Node3 a [Tree3 a]
-- 不存储数据的树结构
data Tree' = Leaf' | Node' Tree' Tree' deriving (Show)
卡特兰树问题是指一个数列,其它数列的第n个值可以表示n个节点所能表示的树的数量,可以使用如下计算:
-- 卡特兰树问题
-- 给定节点个数,返回所有可能的树
trees :: Int -> [Tree']
trees 0 = [Leaf']
trees n = [Node' lt rt | x<-[0..(n-1)],lt <- trees x, rt <- trees $ n-x-1]
--map length $ map trees [0..10] => [1,1,2,5,14,42,132,429,1430,4862,16796]
霍夫曼编码是一种压缩编码方式,他的思想是将出现频率高的字符,使用较短的编码,以节省空间。
-- 霍夫曼编码
-- 基本思路是组合权重最小的两个节点组成一个二叉树
data HTree a = HLeaf a | Branch (HTree a) (HTree a) deriving Show
-- 表示形式为列表,其中每一个元素为二元组,第一个元素为权重,第二为一棵霍夫曼树,但刚开始时,是一个只有一个节点的树
htree :: (Ord w, Num w) => [(w, HTree a)] -> HTree a
htree [(_, t)] = t
htree ((w1,t1):(w2,t2):wts) = htree $ insertBy (comparing fst) (w1+w2, Branch t1 t2) wts
-- 编码
serialize :: HTree a -> [(a, String)]
serialize (HLeaf a) = [(a, "")]
serialize (Branch lt rt) = [(a, '0':s)|(a, s)<-serialize lt] ++ [(a, '1':s)| (a, s)<-serialize rt]
-- huffman
huffman :: (Ord a, Ord w, Num w) => [(w, a)] -> [(a, String)]
huffman [] = []
huffman xs = let t = [(d, HLeaf a)|(d, a) <- xs] in
sortBy (comparing fst) $ serialize $ htree $ sortBy (comparing fst) t
-- huffman [(0.4, "A"),(0.3, "B"), (0.1, "C"), (0.1, "D"), (0.06, "E"), (0.04, "F")] => [("A","0"),("B","10"),("C","1111"),("D","110"),("E","11101"),("F","11100")]
解24点是指将任意4个0~9的数字通过四则运算最终得到结果为24,以下是通过枚举所有可能的算式来求最终的式子:
-- 解24点
-- 定义4则运算的表达式类型
data Exp = Val Double|Plus Exp Exp|Sub Exp Exp | Mult Exp Exp | Div Exp Exp deriving (Show, Eq)
cal :: Exp -> Double
cal (Val a) = a
cal (Plus a b) = cal a + cal b
cal (Sub a b) = cal a - cal b
cal (Mult a b) = cal a * cal b
cal (Div a b) = cal a / cal b
-- 将表达式打印出来
showExp :: Exp -> String
showExp (Val a) = show a
showExp (Plus a b) = "(" ++ showExp a ++ "+" ++ showExp b ++ ")"
showExp (Sub a b) = "(" ++ showExp a ++ "-" ++ showExp b ++ ")"
showExp (Mult a b) = "(" ++ showExp a ++ "*" ++ showExp b ++ ")"
showExp (Div a b) = "(" ++ showExp a ++ "/" ++ showExp b ++ ")"
-- 将列表分成两部分,这两部分的数据可以执行四则运算,然后再对长度大于1的列表再递归划分
divide :: [a] -> [([a],[a])]
divide xs = [(take n xs, drop n xs)| n<- [1..(length xs -1)]]
-- 根据元组,拼合成四则运算
buildExpression :: ([Exp], [Exp]) -> [Exp]
buildExpression (x,y) = [op a b|a<-x, b <-y, op<- [Plus, Sub, Mult, Div]]
-- 将数据数列组合成与任意op结合的表达式
toExpression :: [Double] -> [Exp]
toExpression [] = []
toExpression [x] = [Val x]
toExpression xs = concat [buildExpression (toExpression x, toExpression y)|(x,y) <- divide xs]
-- 使用全排列函数permutations将数字全排列,再对每一个进行toExpression,取出值为24的表达式,并使用showExp展示出来
twentyfour :: [Double] -> [String]
twentyfour xs = [showExp exp |exp<- concatMap toExpression (permutations xs), cal exp == 24.0]
-- twentyfour [7,8,9,6] => ["(8.0/((9.0-7.0)/6.0))","((8.0/(9.0-7.0))*6.0)","(6.0*(8.0/(9.0-7.0)))","((6.0*8.0)/(9.0-7.0))","(8.0*(6.0/(9.0-7.0)))","((8.0*6.0)/(9.0-7.0))","(6.0/((9.0-7.0)/8.0))","((6.0/(9.0-7.0))*8.0)"]
Zipper类型
Zipper类型可以向前或者向后遍历列表,其实现方式是保存了两个两个列表,即当前位置之前的列表,和当前位置之后的列表。
-- 用于可以前后遍历列表的Zipper类型
data Zipper a = Zipper [a] a [a] deriving Show
-- 从数组转到Zipper类型
fromList :: [a] -> Zipper a
fromList (x:xs) = Zipper [] x xs
fromList _ = error "empty list"
-- 用于获取下一个元素和前一个元素
next,prev :: Zipper a -> Zipper a
next (Zipper ys y (x:xs)) = Zipper (y:ys) x xs
next z = z
prev (Zipper (y:ys) x xs) = Zipper ys y (x:xs)
prev z = z
-- next $ next $ fromList [1..10] => Zipper [2,1] 3 [4,5,6,7,8,9,10]
-- 基于树类型的拉锁(Zipper)
-- 树的定义在前面:data Tree a = Leaf a | Node a (Tree a) (Tree a)
data Accumulate a = Empty | R (Accumulate a) a (Tree a) | L (Accumulate a) a (Tree a)
type ZipperTree a = (Tree a, Accumulate a)
-- 三种遍历操作,左分支,右分支,上一层
left,right,up :: ZipperTree a -> ZipperTree a
left (Node a l r, accu) = (r, R accu a l)
left a = a
right (Node a l r, accu) = (l, L accu a r)
right a = a
up (r, R accu a l) = (Node a l r, accu)
up (l, L accu a r) = (Node a l r, accu)
up z@(t, Empty) = z
-- 前面的ZipperTree是使用参数化类型来暂存,也可以使用列表来暂存
data BranchTree1 a = R1 a (Tree a) | L1 a (Tree a)
type ZipperTree1 a = (Tree a, [BranchTree1 a])
left1,right1,up1 :: ZipperTree1 a -> ZipperTree1 a
left1 (Node n l r, t) = (l, L1 n r : t)
left1 z@(Leaf a, t) = z
right1 (Node n l r, t) = (r, R1 n l : t)
right1 z@(Leaf a, t) = z
up1 (r, R1 n l:t) = (Node n l r, t)
up1 (l, L1 n r:t) = (Node n l r, t)
up1 z@(l, []) = z
以上定义的Accumulate类型与[BranchTree1]类型是同构的。Empty相当于空列表([]),R … a (Tree a) 相当于R1 a (Tree a) : [..],而L … a (Tree a)相当于L1 a (Tree a): [..]。
一般化的代数数据类型(GADT)
代数数据类型(Algebraic data type)是指由其他类型通过积类型(product)、和类型(sum)还有函数类型等方式构造出来的类型。
一般化的代数数据类型,可以让构造器携带更多的类型信息来对类型做出一些需要的限制,其它格式为:
data TypeName arg1 arg2 ... where
Con1 :: Type1
Con2 :: Type2
...
我们定义一个具有Int、Bool、加法表达式和判等表达式的类型:
-- 使用一般化的代数类型GADTs
-- 需要在文件开头添加{-# LANGUAGE GADTs #-}来打开选项,GHCi中使用:set -XGADTs
-- 定义一个具有Int、Bool、加法表达式、判等表达式的类型
data Expg a where
ValInt :: Int -> Expg Int
ValBool :: Bool -> Expg Bool
Add :: Expg Int -> Expg Int -> Expg Int
Equa :: Expg Int -> Expg Int ->Expg Bool
evalg :: Expg a -> a
evalg (ValInt a) = a
evalg (ValBool a) = a
evalg (Add a b) = evalg a + evalg b
evalg (Equa a b) = evalg a == evalg b
-- 与非GADTs的写法区别
data Exp' = ValInt' Int | ValBool' Bool | Add' Exp' Exp' | Equa' Exp' Exp'
eval' :: Exp' -> Either Int Bool
eval' (ValInt' a) = Left a
eval' (ValBool' a) = Right a
eval' (Add' a b) = case eval' a of
Left a -> case eval' b of
Left b -> Left (a+b)
eval' (Equa' a b) = case eval' a of
Left a -> case eval' b of
Left b -> Right (a==b)
-- eval' (Add' (ValInt' 10) (ValBool' True))表达式在编译期是不报错的,只有在运行时会报Non-exhaustive patterns
-- 而evalg (Add (ValInt 10) (ValBool True))在编译期就会报错,类型不匹配
从上面的例子可以看出,使用GADTs方式可以在编译器做更多的检查,因为GADT定义的数据类型时给出了每一个数据构造器的类型,而常规方法中这一部分是由编译器自动生成的。
类型的kind
kind是将类型进行分类,在GHCi中使用:t命令来查看。
Prelude> :k Either
Either :: * -> * -> *
Prelude> :k Num
Num :: * -> Constraint
Prelude> :k Int
Int :: *
Prelude> :k Maybe
Maybe :: * -> *
Prelude>
@todo 本章节许多内容不甚了解,所以略过此部分,后续有体会再来补充。
类型类
具有同一性质或者属性的类型可以归为一类,称之为类型类(typeclass),这些属性指的是预先设定好的函数。类型类使用关键字class定义。
import Prelude hiding ((/=), (==),(<=),(>=),(<),(>),compare, Ordering, GT, EQ, LT)
-- 定义一个自定义的MyEq类,与标准库中的Eq类一致
class MyEq a where
(==),(/=) :: a -> a ->Bool
x == y = not (x /= y)
x /= y = not (x == y)
-- 定义一个自定义的类型
data MyNum = O | Zero | One
-- 实现MyEq这个类型类,因为定义中==和/=是互相定义的,所以,只要定义一个==相当于定义了/=
-- 实现类型类的语法为: instance 类型类 类型 where 函数定义 。这里的函数定义如果在类型类中已经定义了,可以省略
instance MyEq MyNum where
O == Zero = True
Zero == O = True
O == O = True
Zero == Zero = True
One == One = True
_ == _ = False
-- [O==Zero,Zero/=Zero,One==O, One /= Zero] => [True,False,False,True]
-- 对于参数化的类型,实现类型类时,可以使用参数限定的方式来定义
instance (MyEq m) => MyEq (Maybe m) where
Just x == Just y = x == y
Nothing == Nothing = True
_ == _ = False
-- Just O == Just Zero => True
-- 在定义类型类时,可以加入对这个类型类的约束,也就是类型类间的依赖关系。注意类型间的依赖不能形成环!
-- 先定义Ordering类型,并实现MyEq类型类
data Ordering = LT | EQ | GT
instance MyEq Ordering where
LT == LT = True
EQ == EQ = True
GT == GT = True
_ == _ = False
-- 定义依赖于MyEq类型类的MyOrd类型类,这里的定义与Prelude里的Ord定义基本一致
class (MyEq a) => MyOrd a where
compare :: a -> a -> Ordering
(<), (<=), (>=), (>) :: a -> a -> Bool
max, min :: a -> a -> a
compare x y
| x == y = EQ
| x <= y = LT
| otherwise = GT
x <= y = compare x y /= GT
x < y = compare x y == LT
x >= y = compare x y /= LT
x > y = compare x y == GT
max x y
| x <= y = y
| otherwise = x
min x y
| x <= y = x
| otherwise = y
-- 以上可以看出<= 与compare是互相定义的,所以实现时,只要定义一个即可
其它常用的类型类
以下这些类型类都定义在Prelude里,我们来看一下他们具体的定义:
class Bounded a where
minBound :: a
maxBound :: a
一般来说Bounded都是可以实现Enum类型类,但Enum却不一定有边界,例如Integer类型。
class Enum a where
succ, pred :: a -> a
toEnum :: Int -> a
fromEnum :: a -> Int
enumFrom :: a -> [a] -- [n..]
enumFromThen :: a -> a -> [a] -- [n,n'..]
enumFromTo :: a -> a -> [a] -- [n..m]
enumFromThenTo :: a -> a -> a -> [a] -- [n,n'..m]
-- Minimal complete definition:
-- toEnum, fromEnum
--
-- NOTE: these default methods only make sense for types
-- that map injectively into Int using fromEnum
-- and toEnum.
succ = toEnum . (+1) . fromEnum
pred = toEnum . (subtract 1) . fromEnum
enumFrom x = map toEnum [fromEnum x ..]
enumFromTo x y = map toEnum [fromEnum x .. fromEnum y]
enumFromThen x y = map toEnum [fromEnum x, fromEnum y ..]
enumFromThenTo x y z =
map toEnum [fromEnum x, fromEnum y .. fromEnum z]
Enum类型类的函数定义都是依赖于toEnum和fromEnum这两个函数,所以实现了Int和类型的互换就可以实现Enum类型类了。
class Show a where
showsPrec :: Int -> a -> ShowS
show :: a -> String
showList :: [a] -> ShowS
-- Mimimal complete definition:
-- show or showsPrec
showsPrec _ x s = show x ++ s
show x = showsPrec 0 x ""
showList [] = showString "[]"
showList (x:xs) = showChar '[' . shows x . showl xs
where showl [] = showChar ']'
showl (x:xs) = showChar ',' . shows x .
showl xs
Show类型可以通过deriving关键字来实现,还可以通过定义show或者showsPrec来实现,标准库中还定义了一些其它的类型和方法:
type ShowS = String -> String
shows :: (Show a) => a -> ShowS
shows = showsPrec 0
showChar :: Char -> ShowS
showChar = (:)
showString :: String -> ShowS
showString = (++)
Functor类型类
-- Functor函子类型类
-- 他的做用是将容器里的值通过一个函数映射成另外一个值
-- 这里的参数f为容器类型的构造器,例如列表类型为[]
-- 注意这里实现的类型必须是一个容器,即kind必须为*->*才行,像Either这种*->*->*的就无法实现Functor
class MyFunctor f where
fmap' :: (a->b) -> f a -> f b
-- 将Maybe实现为Functor类型类
instance MyFunctor Maybe where
fmap' func (Just x) = Just (func x)
fmap' func Nothing = Nothing
-- fmap' (+190) (Just 10) => 200
-- 如果硬要将*->*->*实现为函子类型类,则需要提供一个参数出来
-- 例如函数类型(->)是一个*->*->*的类型,则我们可以给出其输入类型(->) r,使其变成*->*类型,这样就可以实现Functor了
instance MyFunctor ((->) r) where
fmap' f g = (\x -> f (g x))
-- 以上这个fmap'通过简化为 f $ g或者 f.g,最终fmap' = .,即复合函数
-- fmap' (+(100::Int)) (+ (20::Int))这就将+20这个函数映射成了\x -> (x+20) + 100
fmap在Prelude里还定义了一个运算符(<$>)。
注意,虽然实现了fmap函数,但如果不满足以下两个定律的话,也不能称之为Functor:
fmap id = id:即使用id函数做映射时,应该保持不变
fmap (f.g) = fmap f . fmap g:即通过一次复合函数的fmap与通过两次各自函数的map结果是一样的,分配律
例如如下这个Container类型:
-- 有问题的函子类型类实现
data Container a = Container a Int deriving Show
instance MyFunctor Container where
fmap' f (Container x i) = Container (f x) (i+1)
-- fmap' id (Container "abc" 1) => Container "abc" 2
-- fmap' (showChar 'a' . showChar 'c') (Container "abc" 1) => Container "acabc" 2
-- (fmap' (showChar 'a') . fmap' (showChar 'c')) (Container "abc" 1) => Container "acabc" 3
Applicative
如果需要计算两个Just Int之和时,我们可能会定义一个函数来实现justSum (Just i) (Just j) = Just (i+j),但Control.Applicative定义了更加通用的方法Applicative类型类:
-- Applicative类型类
class (Functor f) => Applicative f where
pure :: a -> f a
(<*>) :: f (a->b) -> f a -> f b
infixl 4 <*>
instance Applicative Maybe where
pure = Just
(<*>) Nothing _ = Nothing
(<*>) (Just f) (Just a) = Just (f a)
-- (<*>) (Just f) arg = fmap f arg
-- (Just (+10)) <*> Just 2 => Just 12
-- Just (+) <*> Just 2 <*> Just 10 => Just 12
我们来看看以下几个函数的调用过程:
(+) <$> Just 5 <*> Just 10
= Just (5+) <*> Just 10 -- 使用fmap函数(即<$>将+运用到Just 5中变成Just (5+)
= Just (5+10) -- 使用Applicative类型类的方法<*>,变成Just (5+10),即Just15
= Just 15
pure (+) <*> Just 5 <*> Just 10
= Just (+) <*> Just 5 <*> Just 10
= Just 15
在这两种调用方法在库中分别定义了liftA和liftA2来表示他们:
liftA :: Applicative f => (a->b) -> f a -> f b
liftA2 :: Applicative f => (a->b->c) -> f a -> f b -> f c
liftA f a = pure f <*> a
liftA2 f a b = pure f <*> a <*> b
-- liftA (+) (Just 5) <*> Just 10 => Just 15
-- liftA2 (+) (Just 5) (Just 10) => Just 15
以下例子展示了另外两个运算符:
-- *>运算符,返回两个参数的后一个
(*>) :: Applicative f => f a -> f b ->f b
(*>) u v = pure (const id) <*> u <*> v
-- Just 1 *> Just 2 => Just 2
-- <*运算符,返回两个参数的第一个
(<*) :: Applicative f => f a -> f b ->f a
(<*) u v = pure const <*> u <*> v
-- Just 1 *> Just 2 => Just 1
与Functor类型类相同,Applicative类型类也要满足以下定律:
单位元(identity): pure id <*> v = v
复合定律(composition):pure (.) <*> u <*> v <*> w = u <*> (v <*> w)
同态定律(homomorphism):pure f <*> pure x = pure (f x)
互换定律(interchange): u <*> pure y = pure ($ y) <*> u
关于互换定律中使用的$ y,因为$的类型为($) :: (a -> b) -> a -> b,而此时只给了第二个参数,所以($ y)的类型为(a -> b) -> b。
例如如下的例子计算过程:
pure ($ 5) <*> Just (+1)
= Just ($ 5) <*> Just (+1)
= Just (($ 5) (+1)
= Just ((+1) 5)
= Just 6
= Just (+1) <*> pure 5
Alternative类型类
-- Alternative 类型类
-- 此类型类的作用是选取合理的值
class (Applicative f) => Alternative f where
empty :: f a
(<|>) :: f a -> f a -> f a
-- Maybe类型实现Alternative类型类
instance Alternative Maybe where
empty = Nothing
(<|>) Nothing x = x
(<|>) (Just x) _ = Just x
-- Nothing <|> Just 1 <|> Just 7 => Just 1
可以看出empty定义的是<|>运算符的单位元,与<*>运算符的pure id一样。
@todo 书中介绍了列表的Alternative类型类的实现,不是很懂,略过。
简易字符识别器
{-# LANGUAGE LambdaCase #-}
import Control.Applicative
-- 由于typeclass.h已经弄坏了很多基础库的函数和类型类,所以单独起了个文件
-- 简易字符识别器
-- 定义一个新的类型,他的成员runParser是一个将字符串转成对应的类型a和剩下字符串的二元组的函数
-- 例如识别数字的Parser的runParser会将123abc识别成(123,"abc")这种
newtype Parser a = Parser{
runParser :: String -> Maybe (a, String)
}
-- 其实现的Functor类型类,是将最终产生的结果二元组中的第一个值调用参数f函数
instance Functor Parser where
fmap f p = Parser $ \str -> case runParser p str of
Nothing -> Nothing
Just (t, s) -> Just (f t, s)
-- 实现Applicative函数时第一个Parser的runParser运行的结果二元组一个值为a->b的函数,所以需要将这个函数应用于第二个二元组的第一个值上
instance Applicative Parser where
pure a = Parser $ \str -> Just (a, str)
(<*>) a b = Parser $ \str -> case runParser a str of
Nothing -> Nothing
Just (t, s) -> case runParser b s of
Nothing -> Nothing
Just (t2, s2) -> Just (t t2, s2)
-- 使用第一个Parser,如果结果不为Nothing,就了这个值,否则使用第二个Parser
instance Alternative Parser where
empty = Parser $ const Nothing
(<|>) a b = Parser $ \str -> case runParser a str of
Nothing -> runParser b str
Just x -> Just x
-- 引入辅助函数
satisfy :: (Char->Bool) -> Parser Char
-- 这里的\case需要引入{-# LANGUAGE LambdaCase #-},否则可使用\str -> case str of这个等价语法
satisfy f = Parser $ \case
[] -> Nothing
x:xs -> if f x then Just (x, xs) else Nothing
-- runParser (satisfy (=='a') ) "aaaaabc" => Just ('a', "aaaabc")
char :: Char -> Parser Char
char c = satisfy (==c)
这样我们就有了一个可以识别单个字符的Parser类型了,在介绍其它方法之前,我们先来看一下另外两个方法:
some,many :: (Alternative f) => f a -> f [a]
some v = some_v
where many_v = some_v <|> pure []
some_v = (:) <$> v <*> many_v
many v = many_v
where many_v = some_v <|> pure []
some_v = (:) <$> v <*> many_v
@todo 对于这两个函数的运行机制,我想得不太明白,但与之前的Parser相关函数一同使用,可以产生一些效果:
*Main> runParser (many (char 'a')) "aaaabcd"
Just ("aaaa","bcd")
*Main> runParser (many (char 'a')) "bcd"
Just ("","bcd")
*Main> runParser (some (char 'a')) "aaaabcd"
Just ("aaaa","bcd")
*Main> runParser (some (char 'a')) "bcd"
Nothing
-- 使用<*和*>运算符可以产生忽略某些字符的效果
*Main> (runParser $ char '<' *> many (char 'a') <* char '>') "<aaa>"
Just ("aaa","")
-- isDigit需要引入Data.Char
*Main> (runParser $ char '<' *> many (satisfy isDigit) <* char '>') "<123>"
Just ("123","")
有了some和many的帮助,可以很方便地识别出完整的整数
-- 将数字的字符串直接转成Int
-- fmap digitToInt (satisfy isDigit) 取一个字符,转成Int,runParser (fmap digitToInt (satisfy isDigit) ) "123" => Just (1,"23")
-- many digit即取出所有的数字,组成数组runParser (many $ fmap digitToInt (satisfy isDigit) ) "123" => Just ([1,2,3],"")
-- 最后再计算这个数字列表所代表的整数
number :: Parser Int
number = fmap (foldl (\x y -> 10*x +y ) 0) (many digit)
where digit = fmap digitToInt (satisfy isDigit)
-- runParser number "123" => Just (123, "")
-- 识别字符串,这块有点一头雾水
sequ :: Parser a -> Parser [a] -> Parser [a]
sequ x y = Parser $ \str -> case runParser x str of
Nothing -> Nothing
Just (x1, s1) -> case runParser y s1 of
Nothing -> Nothing
Just (y1, s2) -> Just (x1:y1, s2)
parseStr :: String -> Parser String
parseStr strs = foldr sequ (Parser $ \str -> Just ("",str)) [char s | s <- strs]
-- (runParser (parseStr "hello")) "helloworld" => Just ("hello","world")
Read类型类
略
单位半群(Monoid)
对于集合S和基于S的二元运算⊗:S x S -> S,若⊗满足结合律,即(x ⊗ y) ⊗ z = x ⊗ (y ⊗ z),则有序对(S,⊗)称之为半群。若在半群(S,⊗)上存在一个单位元1,那么三元组(S,⊗,1)称之为单位半群。
有很多单位半群的例子,(Bool, &&, True)、(Bool, ||, False)、(Z, *, 1)、(Z, +, 0)这些都是单位半群。
在Haskell中,单位半群的类型类定义如下:
-- 单位半群
class Monoid a where
mempty :: a
mappend :: a -> a -> a
-- Maybe实现的半群类型类
instance Monoid a => Monoid (Maybe a) where
mempty = Nothing
mappend Nothing m = m
mappend m Nothing = m
mappend (Just x) (Just y) = Just (mappend x y)
-- 列表的半群实现
instance Monoid [a] where
mempty = []
mappend = (++)
Foldable类型类
Foldable类型类可以理解为一个容器,实现Foldable的类型可以折叠为一个值,涉及到Data.Monoid和Data.Foldable,其定义如下:
class Foldable t where
foldMap :: Monoid m => (a->m) -> t a -> m
foldMap f = foldr (mappend . f) mempty
foldr :: (a->b->b) -> b -> t a -> b
foldr f z t = appEndo (foldMap (Endo . f) t) z
我们定义一个树的Foldable实现来看看这个类型类的作用:
-- 定义一个树类型,并实现Foldable类型类
data Tree a = Leaf a | Node (Tree a) a (Tree a)
instance Foldable Tree where
foldMap f (Leaf x) = f x
foldMap f (Node l n r) = foldMap f l `mappend` f n `mappend` foldMap f r
可以看出foldMap是将一个容器里值映射成一个Monoid,如果容器里的值是多个,使用Monoid里的mappend操作,将值连接起来,所以我们可以很容易地定义一个将树转成列表的函数:
flatten :: Tree a-> [a]
flatten t = foldMap (\x -> [x]) t
-- 经过Eta简化之后 变成flatten = foldMap (\x -> [x]),另外(\x -> [x])与(:[]等价),所以flatten = foldMap (:[])
-- foldMap (:[]) ( Node (Leaf True) False (Leaf False))=>[True,False,False]
-- 树求和
sumTree :: (Num a) => Tree a -> Sum a
sumTree = foldMap Sum
-- sumTree ( Node (Leaf 3) 2 (Leaf 1)) => Sum {getSum = 6}
折叠函数foldMap有一个二元性定理(duality theorem),二元性是指两种相对立的情形一定存在,并且可以互相转换:
若(M,⊗,u)为单位半群,则foldr ⊗ u xs = foldl ⊗ u xs,此称之为第一二元性定理,其中的xs为有限元素列表;
若存在两个二元运算符⊗,⊕,还有一个e值,满足x ⊗ (y ⊕ z) = (x ⊗ y) ⊕ z,且x ⊕ e = e ⊗ x,则foldr ⊗ e xs = foldl ⊕ e xs,此称之为第二二元定理,是第一定理的更一般形式;
对于所有的有限列表xs,都有foldr f u x = foldl (flip f ) e (reverse xs),此称之为第三二元定理
以上三个定理的意义在于使得foldr和foldl可以相互转化。foldr是通过扩展递归定义的,而foldl是通过尾递归定义的,所以如何使用得当,可以在计算时节省内存空间。
类型类中的类型依赖
之前的定义中我们定义的类型类,都只有一个参数,像class MyEq a where这样,其实可以定义多参数的类型类:
-- 多参数的类型类
-- 需要{-# LANGUAGE MultiParamTypeClasses #-}选项
class GEq a b where
equals :: a -> b -> Bool
data Nat = Zero' | Succ Nat
-- 定义一个Nat类型和列表类型的GEq实现,比较列表的长度是否与Nat相等
instance GEq Nat [a] where
equals = eq
where eq Zero' [] = True
eq (Succ n) (_:xs) = eq n xs
eq _ _ = False
-- equals (Succ (Succ Zero')) [1,2] => True
定义多个参数的类型类的时候,有可能会产生歧义,例如:
-- 多个参数的类型类产生的歧义
class Func a b where
fun :: a -> b
instance Func Int Nat where
fun _ = Zero'
instance Func Int Int where
fun _ = 0
-- 此时使用fun (1::Int)就会报错,因为编译器不知道返回的类型是Nat还是Int
-- 但可以指定返回值的类型来防止歧义(fun (1::Int))::Nat => Zero'
有时候我们需要明确确定了类型a就只有一种类型b的情况与之对应时,就可以声明{-# LANGUAGE FunctionalDependencies #-}来强制保证确定了类型a只能是类型b与之对应:
-- 多参数强制确定时的写法
-- 需要开启{-# LANGUAGE FunctionalDependencies #-}
class Func a b | a->b where
fun :: a -> b
instance Func Int Nat where
fun _ = Zero'
-- 因为已经确定了类型Int必须是与Nat对应,所以以下的语句会报Functional dependencies conflict between instance declarations错
-- instance Func Int Int where
-- fun _ = 0
-- fun (1::Int) => Zero'
-- 多个参数决定
class (Num a, Num b, Num c) => GPlus a b c | a b -> c where
plus :: a -> b -> c
instance GPlus Int Int Float where
plus a b = fromIntegral a + fromIntegral b
instance GPlus Int Double Double where
plus a b = fromIntegral a + b
另外一个限定的例子:
-- 另外一个歧义的例子
-- 如果没有ce -> e的限定,这里的empty1是通不能编译的
class Collection e ce | ce -> e, e -> ce where
empty1 :: ce
insert :: e -> ce -> ce
member :: e -> ce -> Bool
-- 定义一个实现
-- 由于a 和 [a]有依赖关系,所以需要打开{-# LANGUAGE FlexibleInstances #-}
instance Eq a => Collection a [a] where
empty1 = []
insert x xs = x:xs
member = elem
-- 如果没有e->ce的限定,那么insert 'c' empty1会报错
关联类型(associated type)是另一种消除歧义的方式,其实现的结果与类型依赖一致,但有些时候更加灵活。需要开启{-# LANGUAGE TypeFamilies #-}来使用:
-- 使用关联类型
class (Num a, Num b) => GPlus1 a b where
type SumType a b :: *
plus1 :: a -> b -> SumType a b
instance GPlus1 Int Int where
type SumType Int Int = Float
plus1 a b = fromIntegral a + fromIntegral b
instance GPlus1 Int Double where
type SumType Int Double = Double
plus1 a b = fromIntegral a + b
与GPlus对比,少了类型c,而额外定义了类型SumType,并且是通过a,b类型推断出来的。所以一定程度上与|a b -> c是一致的。
定长列表
使用(!!)运算符时,如果超过列表长度就会报错index too large,那么有没有可能在编译器时期就报出来呢。例如我们定义一个类型FList 10 Interger,这种类型由于依赖于值10,所以称之为依赖类型(dependent type),但是Haskell中类型与值是严格区分的,所以不支持这种方式,只能从类型层面来处理。
-- 定长列表
data O = VO
newtype S n = VS n
-- 开启GADTs
data FList n t where
FNil :: FList O t
FCons :: t -> FList n t -> FList (S n) t
类型O代表长度为0,S O表示长度为1,S (S O)表示长度2,依次类推,所以我们使用了不同的类型表示长度。
如上面的定义,Flist O t代表长度为0,而任何的FCons往列表中添加元素,都会在原来的长度上包一层S类型。例如 FCons ‘c’ (FCons ‘d’ FNil)的类型为FList (S (S O)) Char,即长度为2。
有了FList类型,就可以定义编译期检查的index函数fIndex:
-- 定长数组的编译器检查
class FIndex m n where
fIndex :: m -> FList n t -> t
instance FIndex O (S n) where
fIndex VO (FCons x _) = x
instance FIndex m n => FIndex (S m) (S n) where
fIndex (VS m) (FCons _ xs) = fIndex m xs
-- fIndex (VS (VS (VS VO))) $ FCons 'a' (FCons 'b' (FCons 'c' (FCons 'd' FNil))) => 'd'
-- fIndex (VS (VS (VS VO))) $ FCons 'a' (FCons 'b' (FCons 'c' FNil))会报错
类型类Findex m n可以理解为在长度为n的定长列表中查找元素m。
如果m为O即0,则此时的FIndex获取到的就是头节点,他要求给定的FList类型必须是可构造成FCons x _类型的,如果给出一个FNil,则会报错,fIndex VO FNil会报错。
如果m为S类型,则n也必须是S类型,因为如果n是O类型的话,说明已经越界了。m和n都去掉一层,再进行fIndex操作。因为这个计算是类型的计算,所以是发生在编译期内,这就达到了编译期检查的目的。
运行时重载
我们先定义两个形状,一个长方形,一个圆形,他们都实现了HasArea类型类:
-- 运行时重载
-- 定义矩形和圆形
data Rect = Rect Double Double
newtype Circle = Circle Double
class HasArea t where
area :: t -> Double
instance HasArea Rect where
area (Rect a b) = a * b
-- area (Rect 10 2) => 20.0
instance HasArea Circle where
area (Circle r) = pi * r * r
-- area (Circle 1) => 3.141592653589793
那么如何将这两个类型都放入列表呢?因为列表里的元素只支持一种类型,所以我们可以定义一个data Shape = ShapeRect Rect|ShapeCircle Circle来枚举出所有形状,然后使用[ShapeRect (Rect 10 10),ShapeCircle (Circle 10)]即可,但这不利于后续添加新的形状类型。
我们可以使用GADT数据类型来定义:
data Shape' where
Shape' :: HasArea t => t -> Shape'
这样使用Shape’包装一层之后 ,就可以把长方形和圆形加入到同一个列表中:length [Shape’ (Rect 1 2), Shape’ (Circle 1)] => 2。
要计算面积的话,可以让Shape‘实现HasArea类型类:
-- 实现HasArea类型类,这样好计算面积
instance HasArea Shape' where
area (Shape' shape) = area shape
-- map area [Shape' (Rect 1 2), Shape' (Circle 1)] => [2.0,3.141592653589793]
使用GADTs的形式是在构造函数上对类型添加限制,除了已经淘汰的DatatypeContexts外,我们还可以使用Existential类型:
-- 使用此式子时,需要{-# LANGUAGE ExistentialQuantification #-}选项,这看上去与已经被淘汰的{-# LANGUAGE DatatypeContexts #-},都是给参数添加限定
data Shape1 = forall a. (HasArea a) => Shape1 a
-- newtype (HasArea a) => Shape1 a = Shape1 a
-- :t [Shape1 (Rect 1 2), Shape1 (Circle 1)] => [Shape1 (Rect 1 2), Shape1 (Circle 1)] :: [Shape1]
实现可变长参数的加法
Haskell的函数都有着明确的类型签名,一但定义完成,其支持的参数就固定下来了,如果要支持可变长参数的函数,需要与之前定列表一样,在类型上做处理:
-- 可变长参数的加法
class Addition t where
add :: Int -> t
instance Addition Int where
add t = t
instance (Addition t) => Addition (Int -> t) where
add i x = add (x + i)
-- (add (1::Int) (2::Int) (3::Int) (4::Int) (5::Int) )::Int => 15
至于其中的原理,我们理解Int -> t实现了Addition类型类,所以Int -> Int -> t也实现了Addition类型,依此类推,Int->Int->…->t也实现了Addition类型类,所以可在以任意多个Int参数上调用add方法,得到一个Addition类型t,这也是为什么最终要转化成Int的原因。
@todo 这里的求值过程理得不是特别顺,后续有机会再理。
Monad初步
我们先来看一下四则运算的例子:
-- 四则运算的表达式类型
data Exp = Lit Integer | Add Exp Exp | Sub Exp Exp | Mul Exp Exp | Div Exp Exp
eval :: Exp -> Integer
eval (Lit n) = n
eval (Add e1 e2) = eval e1 + eval e2
eval (Sub e1 e2) = eval e1 - eval e2
eval (Mul e1 e2) = eval e1 * eval e2
eval (Div e1 e2) = eval e1 `div` eval e2
-- eval (Mul (Lit 10) (Lit 20)) => 200
上面这个简单的处理函数,忽略了除以0的情况,如果除数为0,则报错,我们需要改进这一点:
-- 处理除以0的情况
safeEval :: Exp -> Maybe Integer
safeEval (Lit n) = Just n
safeEval (Add e1 e2) = case safeEval e1 of
Nothing -> Nothing
Just x -> case safeEval e2 of
Nothing -> Nothing
Just y -> Just (x + y)
safeEval (Sub e1 e2) = case safeEval e1 of
Nothing -> Nothing
Just x -> case safeEval e2 of
Nothing -> Nothing
Just y -> Just (x - y)
safeEval (Mul e1 e2) = case safeEval e1 of
Nothing -> Nothing
Just x -> case safeEval e2 of
Nothing -> Nothing
Just y -> Just (x * y)
safeEval (Div e1 e2) = case safeEval e1 of
Nothing -> Nothing
Just x -> case safeEval e2 of
Nothing -> Nothing
Just 0 -> Nothing
Just y -> Just (x `div` y)
-- safeEval (Div (Lit 10) (Lit 0)) => Nothing
我们只是处理了除数为0的情况,但代码增加了很多,而且大部分为重复内容,我们可以把这重复内容抽离出来:
-- 抽离公共部分
evalSeq :: Maybe Integer -> (Integer -> Maybe Integer) -> Maybe Integer
evalSeq mi f = case mi of
Nothing -> Nothing
Just a -> f a
-- evalSeq (Just 10) $ \x -> Just (x *2) => 20
-- 借助evalSeq,实现四则运算
safeEval1 :: Exp -> Maybe Integer
safeEval1 (Lit n) = Just n
safeEval1 (Add e1 e2) = evalSeq (safeEval1 e1) $ \x -> evalSeq (safeEval1 e2) (\y -> Just (x+y))
safeEval1 (Sub e1 e2) = evalSeq (safeEval1 e1) $ \x -> evalSeq (safeEval1 e2) (\y -> Just (x-y))
safeEval1 (Mul e1 e2) = evalSeq (safeEval1 e1) $ \x -> evalSeq (safeEval1 e2) (\y -> Just (x*y))
safeEval1 (Div e1 e2) = evalSeq (safeEval1 e1) $ \x -> evalSeq (safeEval1 e2) (\y -> if y == 0 then Nothing else Just (x `div` y))
-- safeEval1 (Div (Lit 10) (Lit 5)) => Just 2
这里的evalSeq就运用了Monad的思想,它其实是一个Maybe Monad,接下来我们来看看完整的Maybe Monad。
Maybe Monad
Monad类型类的定义为:
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
return :: a -> m a
fail :: String -> m a
-- Minimal complete definition:
-- (>>=), return
m >> k = m >>= \_ -> k
fail s = error s
只要实现了(>>=)和return就可以实现Monad类型类,(>>=)的函数声明与evalSeq一致,而return只是简单地将任意类型转成Monad值。
我们来看看Maybe的Monad实现:
instance Monad Maybe where
(Just x) >>= k = k x
Nothing >>= k = Nothing
return = Just
fail s = Nothing
借助Maybe Monad来实现四则运算:
safeEval2 :: Exp -> Maybe Integer
safeEval2 (Lit n) = return n
safeEval2 (Add e1 e2) = safeEval2 e1 >>= \x -> safeEval2 e2 >>= (\y -> return (x + y))
safeEval2 (Sub e1 e2) = safeEval2 e1 >>= \x -> safeEval2 e2 >>= (\y -> return (x - y))
safeEval2 (Mul e1 e2) = safeEval2 e1 >>= \x -> safeEval2 e2 >>= (\y -> return (x * y))
safeEval2 (Div e1 e2) = safeEval2 e1 >>= \x -> safeEval2 e2 >>= (\y -> if y == 0 then Nothing else return (x `div` y))
(>>=)运算符类似于管道,他会将一个第一个参数m a中a的值通过f函数映射成m b的值,而m b的值又可能通过f2函数变成m c,这就使得可以使用(>>=)进行连续的操作。
关键字do和符号<-是实现了>>=操作的语法糖,前面的Add操作,可以写成如下:
safeEval3 (Add e1 e2) = do { x <- safeEval2; y <- safeEval2 e2 ;return x +y}
Monad类型类的实现必须满足以下定律才能具有Monad的特性:
左单位元:
return x >>= f = f x,这个其实就是(>>=)的定义,很容易理解;
右单位元:m >>= return = m,这个通过(>>=)的定义也很容易理解;
结合律:(m >>= f) >>= g = m >>= (\x -> f x >>= g),m的f与g顺序处理,与先将f和g函数合并成一个处理函数,再对m进行处理,效果必须一样 。
列表的Monad实现
-- 列表的Monad的实现
instance Monad [] where
return x = [x]
(>>=) xs f = concatMap f xs
可以琢磨一下这人式子do { x<-[1,2,3]; y<-[2,3,4]; return (x+y)},这个式子的结果与[x+y|x<-[1,2,3], y<-[2,3,4]]的结果是一致的。
Monad相关运算符
类似于复合运算符(.)的(<=<)运算符,其签名为:(与(.)对比)
(.) :: (b -> c) -> (a -> b) -> (a -> c)
(<=<) :: Monad a => (b -> m c) -> (a -> m b) -> (a -> m c)
-- (<=<)运算的例子
Prelude Control.Monad> :m +Control.Monad
Prelude Control.Monad> (\x -> Just (x+10)) <=< (\x -> Just (x/10)) $ 10
Just 11.0
另外一个(>=>)运算符:
(>=>) :: Monad a => (a -> m b) -> (b -> m c) -> (a -> m c)
-- 例子
Prelude Control.Monad> (\x -> Just (x+10)) >=> (\x -> Just (x/10)) $ 10
Just 2.0
从上面两个例子可以看出(>=>)的运算顺序是从左到右,而(<=<)的运算顺序是右到左。
MonadPlus
class Monad m => MonadPlus m where
mzero :: m a
mplus :: m a -> m a -> m a
MonadPlus与Alternative有些类似,表示在计算中有一些选择,如果失败返回mzero。与Monad Maybe只要出错就返回Nothing不同,在某些失败的情况可以恢复时,使用MonadPlus。
具体的使用场景此时还不是特别明了,我们先来看一下列表,半群,Maybe实现MonadPlus的代码:
instance MonadPlus m => Monoid (m a) where
mempty = mzero
mappend = mplus
instance MonadPlus [] where
mzero = []
mplus = (++)
instance MonadPlus Maybe where
mzero = Nothing
mplus Nothing x = x
mplus x _ = x
Functor、Applicative与Monad的关系
在Haskell中这三个类型类的依赖关系并不是十分严格,而在数学上Monad则是通过fmap、return、join来定义的:
class Applicative m => Monad m where
return :: a -> m a
join :: m (m a) -> m a
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
return = pure
join mma = mma >>= id
(>>=) ma m = join $ fmap m ma
(>>) ma mb = ma $ >>= \_ -> mb
这里只要定义join或者定义(>>=)即可实现Monad类型。关于更深层的关联,后续看是否有机会体会到。
系统编程及输入与输出
纯函数:对于相同的函数,总是返回相同的结果。
不纯函数:函数返回的结果,与计算机当前的系统状态有关,例如返回当前时间,产生随机数,从键盘读取值,改变计算机存储器状态等。
副作用:函数执行时,不仅计算函数的结果,还连带地引起其它的计算或者反应,例如打印一行文字,从磁盘读取文件等等。
Haskell中变量一但赋值,就不可改变,这一定程序上增加了纯洁性,但与操作系统交互不可避免,由此引入了Monad来解决不纯函数带来的不确定性。
IO Monad
IO Monad的值IO a表示进行一系列操作之后返回类型a的值。
例如getChar函数,从操作系统获取一个Char,与putChar,将一个Char值输出:
Prelude> :t getChar
getChar :: IO Char
Prelude> getChar
a'a'
Prelude> :t putChar
putChar :: Char -> IO ()
Prelude> putChar 'a'
aPrelude>
可以看出getChar类型是IO Char,他从键盘读取一个字节,然后返回,而putChar的类型为Char -> IO (),将输入的Char打印出来,返回一个空的()类型值。
Monad中的运算符可以运用于IO Monad中:
-- 输入值原样输出
Prelude> getChar >>= putChar
-- ()可以理解为void,使用print输出时为()
aaPrelude> putChar 'c' >>= print
c()
另外三个常用的常用的函数:getLine,putStr,putStrLn:
Prelude> :t getLine
getLine :: IO String
-- 从命令行读取一行字符串
Prelude> getLine
HelloWorld
"HelloWorld"
Prelude> :t putStr
putStr :: String -> IO ()
Prelude> :t putStrLn
putStrLn :: String -> IO ()
-- 输出字符串不带换行
Prelude> putStr "helloworld"
-- 输出字符串带换行
helloworldPrelude> putStrLn "helloworld"
helloworld
来看一个完整的程序:
main :: IO()
main = do
putStr "What's your name?"
name <- getLine
putStrLn $ "Hello " ++ name
-- 运行结果
-- ➜ runghc getline.hs
-- What's your name?Lee
-- Hello Lee
main是可执行文件的入口函数,其类型必须为IO ()。
Monad提供了一个可修改内部值的容器IORef,以及修改函数,但这些操作都发生成IO Monad内部。其函数包括以下:(这些方法在Data.IORef包中)
-- 将给定的参数a存入到一个IORef中
newIORef :: a -> IO (IORef a)
-- 从IORef中读取值
readIORef :: IORef a -> IO a
-- 往一个IORef中写入新值
writeIORef :: IORef a -> a -> IO ()
-- 通过一个函数,将原IORef中的值计算成新值
modifyIORef :: IORef a -> (a -> a) -> IO ()
-- 在多线程中的原子操作
atomicModifyIORef :: IORef a -> (a -> (a, b)) -> IO b
-- 弱引用,在垃圾回收之前可用
mkWeakIORef :: IORef a -> IO () -> IO (GHC.Weak.Weak (IORef a))
看一下以下的例子:
import Data.IORef
main :: IO ()
main = do
aRef <- newIORef 10
modifyIORef aRef (+10)
b <- readIORef aRef
print b
writeIORef aRef 100
b <- readIORef aRef
print b
-- 运行结果
-- ➜ runghc ioref.hs
-- 20
-- 100
输入和输出的处理
先介绍一下在Control.Monad中的几个函数:
-- 一直执行某一个动作,例如forever (do {s <- getLine; putStrLn s}) 会一直请求输入东西,原样输出
forever :: Applicative f => f a -> f b
-- when True (putStrLn "324324"),可以看成if没有else分支,执行的结果只能是f ()
when :: Applicative f => Bool -> f () -> f ()
-- unless False (putStrLn "324324"),与when相反,只有条件为False时才执行
unless :: Applicative f => Bool -> f () -> f ()
-- sequence [Just 10, Just 20] => Just [10, 20],就是将多个Monad的值串起来
-- sequence $ replicate 3 getLine会要求输入三行文字,并生成IO [String]类型的结果
sequence :: (Traversable t, Monad m) => t (m a) -> m (t a)
-- 与sequence一样,只是忽略了返回值,例如sequence_ $ replicate 3 (putStrLn "hello!")打印三次hello,返回 IO ()
-- 这里加了下划线,相当于添加了void :: f a -> f ()调用: void (Just 10)=> Just ()
sequence_ :: (Foldable t, Monad m) => t (m a) -> m ()
-- replicateM 3 (putStrLn "hello!")与前面的例子等价,他是结合了replicate和sequence
replicateM :: Applicative m => Int -> m a -> m [a]
-- 忽略replicateM的返回值
replicateM_ :: Applicative m => Int -> m a -> m ()
-- mapM print [1,2,3,4] => [(),(),(),()] :: IO [()]
-- mapM (\x -> Just x) [1,2,3,4] => Just [1,2,3,4],可以看出mapM就是把列表的值经过函数映射后再组成Manod对应的数组
mapM :: (Traversable t, Monad m) => (a -> m b) -> t a -> m (t b)
-- 与mapM一致,忽略返回值
mapM_ :: (Foldable t, Monad m) => (a -> m b) -> t a -> m ()
-- forM与mapM一致,只是参数换了一下顺序
forM :: (Traversable t, Monad m) => t a -> (a -> m b) -> m (t b)
forM_ :: (Foldable t, Monad m) => t a -> (a -> m b) -> m ()
-- liftM (\x -> replicate x 'a') (Just 10) => Just "aaaaaaaaaa",只是将a1里的值映射成r,与liftA类似
liftM :: Monad m => (a1 -> r) -> m a1 -> m r
再来看一下几个在System.Environment里定义的获取操作系统相关参数的函数:
-- 获取当前的环境变量,例如getEnv "PATH"会返回当前的$PATH配置
getEnv :: String -> IO String
-- 返回当前程序执行的参数
getArgs :: IO [String]
-- 获取当前程序的运行名
getProgName :: IO String
我们来看一个完整的例子:
import System.Environment
main :: IO ()
main = do
args <- getArgs
case args of
[] -> putStrLn "empty args"
_ -> do
x <- getProgName
print $ "Program name:" ++ x
print $ "Args:" ++ concatMap (++ ",") args
-- ➜ runghc env.hs argv1 argv2
-- "Program name:env.hs"
-- "Args:argv1,argv2,"
再来看一下几个在System.IO库中定义的与文件相关的函数:
-- 路径为String的别名
type FilePath = String
-- 文件打开的模式,与其它的语言一致,只读,只写,追加,读写,其中追加、读写、只读会在文件存在时创建
data IOMode = ReadMode | WriteMode | AppendMode | ReadWriteMode
-- 读取文件,接收一个文件名,返回文件内容,如果文件不存在就报错
readFile :: FilePath -> IO String
-- 如果文件存在,则用新的内容覆盖,如果不存在就创建,并写入内容
writeFile :: FilePath -> String -> IO ()
-- 在文件末尾追加内容,如果文件不存在就创建
appendFile :: FilePath -> String -> IO ()
-- 以指定的Mode打开文件,获取文件的句柄
openFile :: FilePath -> IOMode -> IO Handle
如果我们得到了一个IO Handle文件的句柄之后,可以使用以下函数来对文件进行操作:
-- 从当前的位置按照SeekMode移动指针
hSeek :: Handle -> SeekMode -> Integer -> IO ()
-- AbsoluteSeek表示从文件开头开始,RelativeSeek是从当前位置移动,SeekFromEnd是从文件结尾开始,hSeek的第三个参数可以是负数
data SeekMode = AbsoluteSeek | RelativeSeek | SeekFromEnd
-- 返回文件指针的位置
hTell :: Handle -> IO Integer
-- 获取当前一个字符,指针前移
hGetChar :: Handle -> IO Char
-- 获取当前行的内容
hGetLine :: Handle -> IO String
-- 获取当前一个字符,指针不变
hLookAhead :: Handle -> IO Char
-- 获取当前位置到剩下的内容
hGetContents :: Handle -> IO String
-- 判断是否到文件的末尾
hIsEOF :: Handle -> IO Bool
-- do { x <- openFile "index.html" ReadMode; hIsEOF x} => False
-- 有两个可用的Handle:stdin和stdout
接下来看一下与缓冲区和输出相关的函数:
-- 缓存区的类型
data BufferMode = NoBuffering | LineBuffering | BlockBuffering (Maybe Int)
-- 设置缓冲区的类型
hSetBuffering :: Handle -> BufferMode -> IO ()
-- 把资源刷新磁盘或者显示器等等
hFlush :: Handle -> IO ()
-- 关闭资源,会自动调用hFlush
hClose :: Handle -> IO ()
-- 输出一个字符到句柄中
hPutChar :: Handle -> Char -> IO ()
-- 输出字符串到句柄中
hPutStr :: Handle -> String -> IO ()
-- 输出字符串到句柄中,并且追加换行
hPutStrLn :: Handle -> String -> IO ()
-- 将做任意的Show类型输出到句柄中
hPrint :: Show a => Handle -> a -> IO ()
-- do { x <- openFile "t" WriteMode; hPutChar x 'd'; hFlush x}
Haskell中的printf定义在Text.Printf中:
-- 与c语言中的printf一致
printf :: PrintfType r => String -> r
-- printf "name %s, price %d\n" "car" 140000 => name car, price 140000
在haskell中实现可变长参数比较麻烦,我们试着实现自己的printf函数:
{-# LANGUAGE FlexibleInstances #-}
-- 在开始前我们先定义一个函数,他的作用其实是最简单的printf 只支持一个%s的情况
myFormat :: Show a => String -> a -> String
myFormat ('%':'s':xs) s = show s ++ xs
myFormat (c:cs) s = c : myFormat cs s
myFormat "" _ = ""
-- myFormat (myFormat "I'm %s, %s years old!" "Lee") 15 => "I'm \"Lee\", 15 years old!"
-- printf可以是以下的这些形式
-- printf :: String -> IO ()
-- printf :: Show u => String -> u -> IO ()
-- printf :: Show u => String -> u -> u -> IO ()
-- 抽离公共的部分,可以定义一个类型类,其方法为String -> t
class MyPrintf t where
myPrintf :: String -> t
-- 以下是第一种情况,String -> IO()的情况,此时的类型即为IO ()
-- 这里必须添加FlexibleInstances才不会报错,因为默认情况下 type class 实例不支持IO ()
instance MyPrintf (IO ()) where
myPrintf = putStrLn
-- 另外其它情况下,可以把Show u -> MyPrintf t实现成MyPrintf,这样 u -> IO() 是MyPrintf , u -> u -> IO() 也是MyPrintf
-- 这样就把所有的printf场景都抽象成了MyPrintf类型类,可以调用myPrintf来求值
instance (Show u, MyPrintf t) => MyPrintf (u -> t) where
-- 由于t的类型是u->t,所以为了返回t,我们在myPrintf又加了一个参数,其中s可以理解成formatstring,而u为参数,调用myFormat s u,即将u应用到s中生成一个字符串
-- 但参数可能还没有应用完全,所以还需要对这个表达式调用myFormat方法,直到走到IO()的基本情形
myPrintf s u = myPrintf (myFormat s u)
星际译王词典
星际词典共有三个文件:
.ifo文件,记录词典的基本信息,如版本号,作者,名称等等
.idx是单词的索引文件,存放单词在.dict文件中的位置 以及释义的长度,格式为<单词>\0<4字节单词在.dict文件中的偏移量><4字节单词在.dict文件中的释义长度>
.dict是存储单词释义的文件。
这些文件可以从这里下载,不过对于dict文件,是压缩的dict.dz文件,所以需要使用dictzip文件解压,由于Mac上没有找到对应的程序,所以使用了ubuntu系统apt-get install dictzip来处理解压的操作。
整个字典程序,转化为haskell的代码如下:
import Data.Char
import System.Environment
import System.IO
-- import qualified强制在使用这个包里的方法或者类型时,需要加上命名空间
import qualified Data.ByteString.Char8 as BS
-- 索引文件的每一个单词格式,每一个单词在索引文件中由三部分组成,单词本身以\0结尾,4字节偏移量,4字节长度
data WordIndex = WordIndex {
word :: String,
offset :: Int,
expLen :: Int
} deriving (Show)
-- 使用二分查找的方式,在索引列表中搜索出对应的单词信息
searchWord :: String -> [WordIndex] -> Maybe WordIndex
searchWord _ [] = Nothing
searchWord s xs | midWord == s = Just mid
| midWord > s = searchWord s left
| otherwise = searchWord s right
where (left, mid:right) = splitAt (length xs `div` 2) xs
midWord = map toLower (word mid)
-- 从索引文件的String中获取索引列表
getIndexList :: String -> [WordIndex]
getIndexList [] = []
getIndexList s = WordIndex w (byteInt o) (byteInt e) : getIndexList left
where w = takeWhile (/='\0') s
off = drop (length w + 1) s
o = take 4 off
e = take 4 (drop 4 off)
left = drop 8 off
-- 由于索引文件中4个字节表示偏移量和长度,所以需要将一个列表转化为整数
byteInt :: String -> Int
byteInt xs = foldr (\x y -> let (pos,c) = x in 2^(pos*8) * ord c + y) 0 arr
where arr = zip [0..] $ reverse xs
main :: IO ()
main = do
arg <- getArgs
n <- getProgName
case arg of
[] -> print $ "Usage: " ++ n ++ " <word>" -- 没有参数时,提示用法
(a:_) -> do -- 只使用第一个参数
-- 以二进制文件的方式打开文件,并且读取其内容,并转化为列表
idxH <- openBinaryFile "./CET4/CET4.idx" ReadMode
idctIdx <- hGetContents idxH
let indexList = getIndexList idctIdx
let result = searchWord a indexList -- 从列表中搜索出结果来
case result of
Nothing -> print $ "word:" ++ a ++ " not found!"
Just wrd -> do -- 接下来在释义文件中查找
dictH <- openFile "./CET4/CET4.dict" ReadMode
hSeek dictH AbsoluteSeek (toInteger $ offset wrd) -- seek到指定的位置
meaning <- BS.hGet dictH (expLen wrd) -- 使用ByteString里的hGet函数,获取指定字节数量的数据
leftStr <- hGetContents dictH
BS.putStrLn meaning -- 返回的ByteString也需要用到ByteString里的putStrLn函数来输出
运行结果:
➜ runghc dict.hs computer
[kəm'pju:tə]
n. 计算机
例句与用法:
In addition to giving a general introduction to computer, the course also provides practical experience.
课程除了一般介绍电脑知识外,还提供实际操作的机会。
We make copies of our computer disks as a safeguard against accidents.
我们复制了计算机磁盘以防意外。
I'm getting a new computer for birthday present.
我得到一台电脑作生日礼物。
I am a computer operator.
我是一名计算机操作人员。
We should be watchful of computer viruses.
我们应该警惕计算机病毒。
This computer company was established last year.
这家电脑公司是去年成立的。
简易异常处理
与异常相关的类型和方法定义在Control.Exception中,最顶级的异常类型为SomeException,定义如下:
data SomeException = forall e. Exception e => SomeException e deriving (Typeable)
这其中的Exception类型类,定义如下:
class (Typeable e, Show e) => Exception e where
toException :: e -> SomeException
fromException :: SomeException -> Maybe e
toException = SomeException
fromException (SomeException e) = cast e
实现了Exception即可自定义异常类型,Exception的方法都有默认的实现,所以自定义异常类如下:
import Control.Exception
import Data.Typeable
data MyException = forall a. Show a => MyException a deriving (Typeable)
instance Show MyException where
show (MyException a) = "MyException: " ++ show a
instance Exception MyException where
data SomeAException = forall a. Show a => SomeAException a deriving (Typeable)
instance Show SomeAException where
show (SomeAException a) = "SomeAException: " ++ show a
instance Exception SomeAException where
data SomeBException = forall a. Show a => SomeBException a deriving (Typeable)
instance Show SomeBException where
show (SomeBException a) = "SomeBException: " ++ show a
instance Exception SomeBException where
-- 测试
-- *Main Control.Exception> throw (MyException 250 ) `catch` \e ->putStrLn $ "catch a Exception:" ++ show (e::MyException)
-- catch a Exception:MyException: 250
-- 由于这个异常也是属于SomeException顶级异常的,所以这块也能正常输出
-- *Main Control.Exception> throw (MyException 250 ) `catch` \e ->putStrLn $ "catch a Exception:" ++ show (e::SomeException)
-- catch a Exception:MyException: 250
-- 如果再定义一个其它的异常,这时时候的catch就无法捕捉到了
-- *Main Control.Exception> throw (SomeAException 250 ) `catch` \e ->putStrLn $ "catch a Exception:" ++ show (e::SomeBException)
-- *** Exception: SomeAException: 250
haskell中用到的try、catch、throw与其它语言不同,这些都不是关键字,而是函数:
try :: Exception e => IO a -> IO (Either e a)
catch :: Exception e => IO a -> (e -> IO a) -> IO a
throw :: Exception e => e -> a
catches :: IO a -> [Handler a] -> IO a
本章节的内容不太好理解,虽然补充学习了《Real World Haskell》错误处理章节,但还是有点朦胧。
时间相关处理函数
与时间相关的函数,由于与当前系统的状态有关,不是纯函数,所以也在IO Monad中处理:
Prelude> :m Data.Time
Prelude Data.Time> :t getCurrentTime
getCurrentTime :: IO UTCTime
Prelude Data.Time> getCurrentTime
2019-09-24 07:41:40.390005 UTC
Prelude Data.Time> do{ ti<- getCurrentTime ; print $ utctDay ti}
2019-09-24
记录器Monad、读取器Monad、状态Monad
记录器Monad
记录器Monad(Writer Monad),是在计算一个类型值的同时,还会使用另外一个类型记录下中间过程。其定义在Control.Monad.Writer中。
例如我们要在x轴上移动某一个点并标记移动过程,可以使用Writer Monad来处理:
import Control.Monad.Writer
left, right :: Int -> Writer String Int
left x = writer (x -1 , "move left\n")
right x = writer (x +1 , "move right\n")
move :: Int -> Writer String Int
move x = do
a <- left x
b <- left a
right b
-- *Main> move 3
-- WriterT (Identity (2,"move left\nmove left\nmove right\n"))
对于其结果,可以看出虽然返回的的是Writer类型,但是却输出为WriterT,这是由于在最新版本的Haskell中Writer是使用WriterT来定义。
对于Writer类型,如果第一个类型(即之前的String)实现了Monoid类型类,此时的Writer才是一个Monad类型,才可以使用do表达式来处理。
writer是构造Writer类型的方便的函数。
这里如何理解do里的语句呢?有一个简单的理解方式就是把do转化为>>=运算。如之前的move函数,可以写成move x = left x >>= left >>= right,而Writer的>>=实现大致为如下:
instance (Monoid w) => Monad (Writer w) where
return x = Writer (x mempty)
(Writer (x,v)) >>= f = let (Writer (y, v')) = f x in
Writer (y, v `mappend` v')
从之前的例子可以看出Writer Monad总是返回计算的结果,而并没有在程序背后保持某一状态,这是与之后介绍的State Monad区别的地方。
MonadWriter
class (Monoid w, Monad m) => MonadWriter w m | m -> w where
tell :: w -> m ()
listen :: m a -> m (a, w)
pass :: m (a, w -> w) -> m a
tell函数只是记录的追加,并不会进行计算,而listen的结果会同时返回计算结果和记录,pass则会对记录器Monad输入一个函数:
-- tell只是在记录中追加,@todo 关于tell函数的原理以及与do结合使用的原理,目前还搞不懂
*Main> do {tell "first move left twice ,then move right\n"; a <- left 3; b <- left a; right b}
WriterT (Identity (2,"first move left twice ,then move right\nmove left\nmove left\nmove right\n"))
-- listen将参数做为值返回
*Main> do {a <- left 10; listen $ right a}
WriterT (Identity ((10,"move right\n"),"move left\nmove right\n"))
-- @todo 这里的pass参数不太明白为什么这样写。。
*Main Data.Char> do{ a<- left 100; b<-pass $writer ((a-1, map toUpper), "pass run");left b}
WriterT (Identity (97,"move left\nPASS RUNmove left\n"))
以下归并排序的例子,使用Writer Monad来记录排序的过程:
-- 归并排序,即将两个已经排好序的列表合并成一个有序的列表
-- 辅助函数,将两个有序的列表合并成一个
mergeSortList ::Ord a => [a] -> [a] -> [a]
mergeSortList [] a = a
mergeSortList a [] = a
mergeSortList (x:xs) (y:ys) | x > y = y : mergeSortList (x:xs) ys
| otherwise = x : mergeSortList xs (y:ys)
-- 显示多个空格缩进的函数
indent :: Int -> ShowS
indent n = showString $ replicate (4 * n) ' '
-- 显示空行
nl :: ShowS
nl = showChar '\n'
-- 归并排序,并记录过程
mergeSort :: Int -> [Int] -> Writer String [Int]
mergeSort _ [] = return []
mergeSort _ s@[_] = return s
mergeSort l s@xs = do
tell $ (indent l.showString "mergesort: ".shows s.nl) ""
let (ll,rl) = splitAt (length xs `div` 2) xs
tell $ (indent (l+1).showString "merge".shows ll.shows rl.nl) ""
liftM2 mergeSortList (mergeSort (l+2) ll) (mergeSort (l+2) rl)
-- 运行结果
-- *Main> putStrLn $ execWriter $ mergeSort 0 [5,4,3,6]
-- mergesort: [5,4,3,6]
-- merge[5,4][3,6]
-- mergesort: [5,4]
-- merge[5][4]
-- mergesort: [3,6]
-- merge[3][6]
读取器Monad
import Control.Monad.Reader
readLen :: Reader [a] Int
readLen = reader $ \x -> length x
readHead :: Reader [a] a
readHead = reader $ \(x:_) -> x
-- *Main> runReader readLen "abcdefg"
-- 7
-- *Main> runReader readHead "abcdefg"
-- 'a'
使用reader函数产生一个Monad Reader,其接受一个函数作为参数,使用runReader运行函数获取对应的结果。
MonadReader
MonadReader提供了ask和local函数,ask是获取到当前的Monad Reader,而local接收一个函数,是将第二个参数的Reader应用一次这个函数。如以下例子:
test :: Reader [Int] [Int]
test = do
xs <- local (map (+1)) ask
ys <- ask
return ys
-- *Main> runReader test [1,2,3]
-- [1,2,3]
例子中xs的值为[2,3,4],而ys的值为[1,2,3]。
库中提供了两个封装的函数withReader和mapReader函数来处理以上例子中的情况,我们从两个例子分析中来加深映像:
+1 读取器: reader (+1)
使用withReader函数,将现有的读取器应用一个新函数,使其成为一个新的读取器:withReader (*2) $ reader (+1),注意这个读取器会先应用后传入的函数,即*2,再应用+1
使用这个新的读取器:
*Main> runReader (withReader (*2) $ reader (+1)) 10
21
而mapReader与local的功能类似,他不会生成一个新的Reader,只是将Reader应用函数f:
*Main> runReader (mapReader (*2) $ reader (+1)) 10
22
带变量绑定的表达式
-- 带变量绑定的表达式
data Exp = Val Int |
Var String |
Add Exp Exp |
Decl Bind Exp deriving (Show, Eq)
type Bind = (String, Int)
type Env = [Bind]
updateEnv :: Bind -> Env -> Env
updateEnv = (:)
resolve :: Exp -> Reader Env (Maybe Int)
resolve (Val i) = return (Just i)
resolve (Var s) = do
env <- ask
case lookup s env of
Nothing -> return Nothing
Just v -> return (Just v)
resolve (Add e1 e2) = do
re1 <- resolve e1
case re1 of
Nothing -> return Nothing
Just a -> do
re2 <- resolve e2
case re2 of
Nothing -> return Nothing
Just b -> return (Just (a+b))
resolve (Decl b e) = local (updateEnv b) (resolve e)
-- *Main> runReader (resolve (Decl ("x", 3) (Decl ("y", 5) (Add (Var "y") (Add (Var "x") (Var "z"))))) ) [("z", 4)]
-- Just 12
状态Monad
状态Monad所接收的参数也是一个函数,传入一个状态,返回一个值和新状态的二元组。
通过遍历标记二叉树的方式,我们来看一下状态Monad的使用:
import Control.Monad.State
data Tree a = Leaf a | Node (Tree a) a (Tree a) deriving (Show, Eq)
-- 不使用状态Monad时的程序
labelTree :: Tree a -> Tree (a, Int)
labelTree t = fst $ ntAux t 0
ntAux :: Tree a -> Int -> (Tree (a,Int), Int)
ntAux (Leaf a) n = (Leaf (a, n), n+1)
ntAux (Node l a r) n = let (lt, n') = ntAux l (n+1) in
let (rt, n'') = ntAux r n' in
(Node lt (a, n) rt, n'')
-- 使用状态Monad来处理
labelTree' :: Tree a -> Tree (a, Int)
labelTree' t = evalState (ntAux' t) 0
increase :: State Int Int
increase = state $ \i -> (i, i+1)
ntAux' :: Tree a -> State Int (Tree (a, Int))
ntAux' (Leaf a) = do
n1 <- increase
return (Leaf (a, n1))
ntAux' (Node l n r) = do
n1 <- increase
lt <- ntAux' l
rt <- ntAux' r
return (Node lt (n, n1) rt)
-- *Main> labelTree' $ Node (Node (Leaf 5) 3 (Leaf 2)) 7 (Leaf 9)
-- Node (Node (Leaf (5,2)) (3,1) (Leaf (2,3))) (7,0) (Leaf (9,4))
-- *Main> labelTree $ Node (Node (Leaf 5) 3 (Leaf 2)) 7 (Leaf 9)
-- Node (Node (Leaf (5,2)) (3,1) (Leaf (2,3))) (7,0) (Leaf (9,4))
与传统的方法不同的是,程序中不再管理当前的值,而是代理给了状态Monad来管理。
使用状态Monad实现栈结构
-- 使用状态Monad来实现栈结构
type Stack = [Int]
pop :: State Stack Int
pop = state $ \(x:xs) -> (x, xs)
push :: Int -> State Stack ()
push n = state $ \xs -> ((), n:xs)
peek :: State Stack Int
peek = state $ \(x:xs) -> (x, x:xs)
test :: State Stack Int
test = do
push 1
push 2
push 3
a1 <- pop
a2 <- pop
return (a1 + a2)
-- *Main> runState test []
-- (5,[1])
状态Monad、FunApp单位半群和读取器Monad的关系(略)
MonadState状态类(略)
基于栈的计算器(略)
随机数的生成(略)
Monad转换器
先介绍一下Identity。Identity是一个没有任何行为的类型,实现了Monad类型类,所以不管是在Monad转器中还是在函数需要Monad参数时都可以使用此类型,它的定义为:
newtype Identity a = Identity { runIdentity :: a }
Identity对应的Monad转化器为IdentityT,其定义为:
-- 自己构造的Identity的Monad转化器
newtype IdentityT m a = IdentityT { runIdentityT :: m a }
-- 要将IdentityT m实现Monad类型类,根据Monad类型类的实现
-- class Monad m where
-- (>>=) :: m a -> (a -> m b) -> m b
-- return :: a -> m a
-- 此时的IdentityT m实现Monad类型类的(>>=)和return类型为:
-- return :: a -> IdentityT m a
-- (>>=) :: IdentityT m a -> (a -> IdentityT m b) -> IdentityT m b
instance (Monad m) => Monad (IdentityT m) where
return a = IdentityT $ return a
itm >>= k = IdentityT $ do
a <- runIdentityT itm -- runIdentityT itm得到的类型为IdentityT m a中的m,所以a的类型就是a
runIdentityT (k a) -- k a的类型为IdentityT m b,所以这个do语句返回的类型为m b, 而最终>>=需要返回 IdentityT m b,所以最外层需要加一个IdentityT构造函数
-- 这两个Applicative和Functor实现必不可少,不然会报如下错误:
-- • Could not deduce (Applicative (IdentityT m))
-- arising from the superclasses of an instance declaration
instance (Monad m) => Applicative (IdentityT m) where
pure = return
(<*>) = ap
instance (Monad m) => Functor (IdentityT m) where
fmap = liftM
转化器的作用是组合使用各种不同的Monad,例如刚刚定义的IdentityT转化器,可以组合Maybe来使用:
-- 使用IdentityT的例子
imi :: IdentityT Maybe Int
imi = IdentityT $ Just 10
imi2 :: IdentityT Maybe Int
imi2 = (>>=) imi $ \x -> IdentityT $ Just (x+10)
这时只是举例说明转化器的组合多种Monad用法,定义的Identity Maybe Int完全与Maybe Int等价,即这两种类型是同构的。
我们再来看看如何使用StateT和MaybeT来处理栈pop操作中,栈为空的异常情况:
-- 使用StateT和Maybe来处理push和pop
-- newtype StateT s (m :: Type -> Type) a
-- 构造函数为:StateT (s -> m (a, s))
pushSM :: Int -> StateT [Int] Maybe ()
pushSM n = StateT $ \xs -> Just ((), n:xs)
popSM :: StateT [Int] Maybe Int
popSM = StateT $ \case
[] -> Nothing
x:xs -> Just (x, xs)
-- *Main> runStateT popSM []
-- Nothing
-- 使用MaybeT和State来处理push和pop
-- newtype MaybeT m a
-- MaybeT
-- runMaybeT :: m (Maybe a)
pushMS :: Int -> MaybeT (State [Int]) ()
pushMS n = MaybeT $ state $ \xs -> (Just (), n:xs)
popMS :: MaybeT (State [Int]) Int
popMS = MaybeT $ state $ \case
[] -> (Nothing, [])
x:xs -> (Just x, xs)
-- *Main> runState (runMaybeT popMS ) []
-- (Nothing,[])
从两个例子的结果上可以看出使用MaybeT State组合时,如果出错,可以保留栈的状态。
再来看一下不使用转换器,而使用State和Maybe Int组合来实现的pop:
-- 使用State和Maybe Int组合来处理问题
pushSM' :: Int -> State [Int] (Maybe ())
pushSM' n = state $ \xs -> (Just (), n:xs)
popSM' :: State [Int] (Maybe Int)
popSM' = state $ \case
[] -> (Nothing, [])
x:xs -> (Just x, xs)
-- *Main> runState popSM' []
-- (Nothing,[])
-- 比较组合与转换器之间在处理上的区别
-- 可以看出由于转换器在do中直接取出的类型就是Int,所以不需要进行一次模式匹配
tSM' :: State [Int] (Maybe Int)
tSM' = do
pushSM' 5
a <- popSM'
case a of
Nothing -> return Nothing
Just x -> return $ Just (x+1)
tMS :: MaybeT (State [Int]) Int
tMS = do
pushMS 5
a <- popMS
return (a+1)
Monad转换器的组合顺序 (略)
lift和liftIO (略)
简易Monad编译器(略)
语法分析Monad组合子(略)
QuickCheck简介
需要下载QuickCheck包cabal update;cabal install QuickCheck,这个测试库可以在一定程序上生成测试用例。
import Test.QuickCheck
prop_even x y = even (x+y) == (even x == even y)
-- 自动生成100个测试用例,并测试通过
-- *Main> quickCheck prop_even
-- +++ OK, passed 100 tests.
prop_reverse xs ys = reverse ys ++ reverse xs == reverse (xs ++ ys)
-- *Main> quickCheck prop_reverse
-- +++ OK, passed 100 tests.
prop_reverse_twice xs = (reverse.reverse) xs == xs
-- *Main> quickCheck prop_reverse_twice
-- +++ OK, passed 100 tests.
-- 判断列表是否是有序
ordered :: Ord a => [a] -> Bool
ordered [] = True
ordered [_] = True
ordered (x:y:ys) = x <= y && ordered (y:ys)
-- 选择排序,即每一次遍历取出最小的一个放在开头
selectionSort :: Ord a => [a] -> [a]
-- 辅助函数,从列表中取出最小的值,并删除这个元素
selectionSortMin :: Ord a => [a] -> (a, [a])
selectionSortMin [a] = (a, [])
selectionSortMin (x:y:xs) | x > y = let (min, dest) = selectionSortMin(y:xs) in (min, x:dest)
| otherwise = let (min, dest) = selectionSortMin(x:xs) in (min, y:dest)
selectionSort [] = []
selectionSort xs = let (min, dest) = selectionSortMin xs in min:selectionSort dest
prop_sort xs = ordered $ selectionSort xs
-- *Main> quickCheck prop_sort
-- +++ OK, passed 100 tests.
-- 在进行排序后的列表首元素为最小元素的测试时,如果没有限定列表不为空,则会出现失败的情况
prop_headMin xs = head (selectionSort xs) == minimum xs
-- *Main> quickCheck prop_headMin
-- *** Failed! Exception: 'Prelude.head: empty list' (after 1 test):
-- []
-- 需要使用(==>)来限定测试集中不能有空列表
prop_headMin' ::Ord a => [a] -> Property
prop_headMin' xs = not (null xs) ==> head (selectionSort xs) == minimum xs
-- *Main> quickCheck prop_headMin'
-- +++ OK, passed 100 tests; 15 discarded.
除了使用quickCheck来进行测试外,如果需要展示更多的信息,可以使用verboseCheck:
*Main> verboseCheck prop_even
Passed:
0
0
...
Passed:
15
85
+++ OK, passed 100 tests.
测试数据生成器
对于自定义的类型,可以实现Arbitray类型类来自动生成测试数据:
class Arbitray a where
arbitray ::Gen a
另外库是提供了一些常用的函数来供使用:
-- 从列表中的值中随机选取一个
elements :: [a] -> Gen a
-- 从一个范围内随机生成一个值
choose :: System.Random.Random a => (a, a) -> Gen a
-- 从多个生成 品随机抽取一个
oneof :: [Gen a] -> Gen a
例如我们有一个算术表达式类型,我们需要随机生成一些算术表达式:
newtype Exp = Exp String deriving (Show, Eq)
-- Exp = Int | Exp op Exp
instance Arbitrary Exp where
arbitrary = do
n <- choose (0,1) :: Gen Int
case n of
0 -> do
num <- choose (0,100) :: Gen Int
return $ Exp (show num)
1 -> do
op <- elements ["+", "-", "*", "/"]
Exp exp1 <- arbitrary :: Gen Exp
Exp exp2 <- arbitrary :: Gen Exp
return $ Exp (exp1 ++ op ++ exp2)
-- *Main> sample (arbitrary :: Gen Exp)
-- Exp "34"
-- Exp "94"
-- Exp "15"
-- Exp "85-58*66"
-- Exp "81-3+30-83"
-- Exp "78+55/78*42+75/55+24/65*50/76*43+32*92*59*97/65/23/96*94/98/1*34-61/41*90+50+68"
-- Exp "85"
-- Exp "42+84"
-- Exp "34"
-- Exp "42"
-- Exp "96*77*24+12/18"
惰性求值简介
λ演算简介
λ演算由数学家Alonzo Church引入,虽然简单,但可以看做是一个完整的编程语言:
Expression -> Constant
| Variable
| Expression Expression
| λ Variable. Expression
这其中Constant为常量;Variable为变量名称,约定使用小写字母;Expression Expression可以理解为函数应用;λ Variable. Expression则为λ函数定义,称为λ抽象。
在λ函数定义中,如果变量x引入到函数体t中,则称x在t内被限定了,如果没有,则称些变量为游离的,没有游离变量的λ函数称之为闭合的,否则为开放。
λ抽象默认为右结合性,而函数默认为左结合性,所以表达式λx. λy. λz.x y z为(λx. (λy. (λz.(x y) z )))
之前我们讨论过λ表达式的转换和简化,这里复习一下:
α替换(α-conversion):α替换是指在命名不冲突的前提下可以将函数的参数重新命名。
β简化(β-reduction):β简化是指将参数应用于函数体。
η简化(η-reduction):η简化可以消除冗余的λ表达式。
如果一个λ表达式不能再进行β简化,则称之为β常态形式(β-normal form),简写为β-nf,如果连η简化也不能进行,称之为βη-nf。
⊥ Bottom
⊥表示不可能完成的计算结果。在haskell中可以表示为forever的结果、异常、undefined等等。
在使用data来定义类型时,会自动添加⊥值来表示计算的失败或者不可终止,例如我们可以说 1 div 0 = ⊥。包含⊥值的类型称之为lifted。
newtype不会引入⊥:
newtype N = N Int
data D = D Int
n (N i) = 42
d (D i) = 42
-- *Main> n undefined
-- 42
-- *Main> d undefined
-- *** Exception: Prelude.undefined
-- CallStack (from HasCallStack):
-- error, called at libraries/base/GHC/Err.hs:78:14 in base:GHC.Err
-- undefined, called at <interactive>:3:3 in interactive:Ghci2
可以看出包含⊥值的类型D在使用函数d求值时,由于d ⊥ = ⊥,所以会直接报错。
如果一个函数是严格的,那么当且仅当f ⊥ = ⊥。即参数求值失败,则f的计算也会不成功。haskell为非严格语言,例如n ⊥ = 42。
由于惰性求值,所以某些时候虽然参数为⊥,但结果并非⊥。
-- 惰性求值对计算结果的影响
data D2 = D2 !Int
d2 (D2 i) = 42
-- *Main> d2 (D2 undefined)
-- *** Exception: Prelude.undefined
-- CallStack (from HasCallStack):
-- error, called at libraries/base/GHC/Err.hs:78:14 in base:GHC.Err
-- undefined, called at <interactive>:14:8 in interactive:Ghci1
-- *Main> d (D undefined)
-- 42
在const函数中直接返回第一个参数的值,而不会求值第二个参数,而seq在返回第二个参数之前,会严格计算第一个参数的值,如果第一个参数为⊥,则返回值也为⊥。
*Main> const 1 undefined
1
*Main> seq undefined 1
*** Exception: Prelude.undefined
CallStack (from HasCallStack):
error, called at libraries/base/GHC/Err.hs:78:14 in base:GHC.Err
undefined, called at <interactive>:24:5 in interactive:Ghci8
表达式形态与trunk
关于WHNF、HNF、NF这些的区别可以参考这里。
NF值那些已经不能简化了的表达式,而WHNF指的是那些最外层的表达式是一个值构造器或者是匿名函数。
可以看出WHNF包含了NF。这些概念在分析哪些表达需要立刻求值,哪些表达可以延后求值上很重要。
-- 以下是NF
42
(2, "hello")
\x -> (x + 1)
--以下不是NF
1 + 2 -- 我们可以把它求值为 3
(\x -> x + 1) 2 -- 我们可以应用这个函数
"he" ++ "llo" -- 我们可以应用 (++)
(1 + 1, 2 + 2) -- 我们可以对 1 + 1 以及 2 + 2求值
-- 以下是WHNF
(1 + 1, 2 + 2) -- 最外层是一个值构造器 (,)
\x -> 2 + 2 -- 最外层是一个匿名函数的抽象
'h' : ("e" ++ "llo") -- 最外层是一个值构造器 (:)
-- 以下不是WHNF
1 + 2 -- 最外层是 (+) 函数的调用
(\x -> x + 1) 2 -- 最外层是匿名函数 (\x -> x + 1) 的调用
"he" ++ "llo" -- 最外层是 (++) 函数的调用
trunk意为形实替换程序,指的是以一段程序来代表一些函数的参数或者一些结果。这个表达式与环境形成了一个无参数的闭包,包含了所有计算结果所需要的所有信息。在惰性求值中会尽量延后对表达式的求值,而是以trunk形式来代替,在必要时根据这个闭包环境来求值。
在GHCi中使用:sprint命令可以在打印结果时不严格地求值,对于未求出的部分使用下划线表示,@todo 这块在我的GHCi上并不能很好的体现,先略过。
求值策略
引用求值:call by value,即在调用一个函数前,先把参数的值求出后再传入函数,这也是最常见的方式。
按名调用:call by name,即将参数直接替换到函数体中,如果这个参数在函数体里没有参与计算,则这个参数就不会被计算。
常序求值:normal order evaluation,从左边最外侧的不在λ函数定义内部的式子开始计算。
并行与并发编程
并发编程相关的包为monad-par,可以通过cabal install monad-par安装。
我们通过f (g x) (h x)这个表达中的g x 和 h x的并行计算来展示haskell中并发编程的要点。
这时里假定这两个并行计算的函数都是绑定某个数是否为素数,而f为这两个素数的乘积,如果不是素数返回0.
import Control.Monad.Par
isPrime ::Integer -> Bool
isPrime 2 = True
isPrime n = n > 1 && all (\x -> (n `mod` x) /= 0) (takeWhile (\x -> x * x < n) $ 2:[3,5..])
generateKey :: Integer -> Integer -> Integer
generateKey x y = runPar $ do
k1 <- new
k2 <- new
-- 不知道为什么下面这句话会报错
-- [k1,k2] <- sequence [new, new]
fork $ put k1 (isPrime x)
fork $ put k2 (isPrime y)
p1 <- get k1
p2 <- get k2
return $ if p1 && p2 then x * y *10 else 0
main = print $ generateKey 2646507710984041 1066818132868207
-- main = do
-- print $ isPrime 2646507710984041
-- print $ isPrime 1066818132868207
-- print $ 2646507710984041 * 1066818132868207 *10
轻量级线程
import Control.Concurrent
import Control.Monad
import System.IO
main :: IO ()
main = do
hSetBuffering stdout LineBuffering
_ <- forkIO $ replicateM_ 20 (putStrLn "thread 1")
_ <- forkIO $ replicateM_ 20 (putStrLn "thread 2")
return ()
–
结语
haskell这本书一直都想看完,但每一次都是看完几章节之后就放弃了。这大概源于函数式编程语言的不习惯与对算法问题以及数学问题及思维的不敏感。
这次强制以笔记的形式大概读完了,从头到尾也花了将近2个月的时间,但中间有很多略过的以及不甚理解的部分,并非没有细细琢磨,而是实在需要更多的练习与实践才能形成一种对语言的条件反射。
另外对于函数式编程的诸多优点,我可能只理解了纯函数、惰性求值等并不深入的部分,而更加本质化的,更加深入化的一面,如同之前所说,需要在有机会实践或者从事这方面时才能更进一步了解。
本书的结尾草草结束,最后一章节的内容省略了一大半,出于多种原因,细细品味的动力确实不足,只能以此草草结束。这篇文章这本书或者这是我函数式编程的开端,当然也可能是最后的一次这么系统的学习了。