Lecture1: Clustering
无监督学习:介绍
无监督学习的样本区别于有监督学习的是每一个样本没有标签。
如有监督学习的样本表示为\(\{(x^{(1)}, y^{(1)}),(x^{(2)},y^{(2)}),(x^{(3)},y^{(3)}),\cdots,(x^{(m)},y^{(m)})\}\)
则无监督学习的样本表示为\(\{x^{(1)}, x^{(2)},x^{(3)},\cdots,x^{(m)}\}\)
- 应用
市场划分(Market segmentation)
社交网络划分(Social network analysis)
组织计算机集群(Organizing computer clusters)
天文数据分析(Astronomical data analysis)
K-均值算法(K-Means Algorithm)
基本步骤
- 随机选取两个点(分为两类),这两个点称之为聚类中心(cluster centroids)
- 聚类分配:将样本数据根据距离聚类中心的远近分成两类
- 移动聚类中心:根据聚类分配划分的两个集合,算出各自的均值,将聚类中心移至该点
- 重复聚类分配和移动聚类中心两个步骤,直到聚类中心不再变化
变量符号定义
\(K\):分类的数量
样本集:\(\{x^{(1)}, x^{(2)},x^{(3)},\cdots,x^{(m)}\}\)
其中\(x^{(i)} \in \mathbb{R}^n\),即没有\(x_0\)
算法描述
Randomly initialize K cluster centroids mu(1), mu(2), ..., mu(K)
Repeat:
for i = 1 to m:
c(i):= index (from 1 to K) of cluster centroid closest to x(i)
for k = 1 to K:
mu(k):= average (mean) of points assigned to cluster k
- 第一个循环是聚类分配步骤,\(c(i)\)表示第i个样本所属于的聚类中心
\(c^{(i)} = argmin_k\ ||x^{(i)} - \mu_k||^2:c^{(i)}\)到\(x^{(i)}\)距离最近的聚类中心
说明:上面式子并非真正的欧几里得距离(Euclidean distance),但与其等价并会减少计算量
- 第二个循环是移动聚类中心步骤
\(\mu_k = \dfrac{1}{n}[x^{(k_1)} + x^{(k_2)} + \dots + x^{(k_n)}]\)
其中\(x^{(k_1)},x^{(k_2)} \cdots\)为聚类中心为\(\mu_k\)的样本
-
如果没有任何样本属于某一个聚类中心,那么可以直接去掉此聚类中心或者再随机选择一个点做为此聚类中心
-
当迭代到一定数量时,聚类中心不再改变,此时算法收敛
-
K-均值算法对于没有明显分开的样本,也能正常的工作,算出k个分类来
优化目标函数(Optimization Objective)
代价函数
\[\class{myMJSmall}{ J(c^{(1)},\cdots,c^{(m)},\mu_1,\cdots,\mu_K) = \frac{1}{m}\sum_{i=1}^{m}||x^{(i)} - \mu_{c^{(i)}}||^2 }\]\(c^{(i)}\):样本\(x^{(i)}\)所属于的聚类中心序号,\(c^{(i)} \in [1,K]\)
\(\mu_k\):第k个聚类中心\(k\in[1,K],\mu_k \in \mathbb{R}^n\)
\(\mu_{c^{(i)}}\):样本\(x^{(i})\)所属于的聚类中心
以上函数也叫做失真代价函数(Distortion Cost Function)
- 我们的优化目标是找出K个聚类中心,使用所有样本到其所属的聚类中心的距离之和最小,即\(min_{c,\mu}\ J(c,\mu)\)
在K-均值算法中,第一步聚类分配步骤,选择适合的\(c^{(i)}\)使得\(J\)最小
在移动聚类中心步骤中,是移动\(\mu_k\)使得\(J\)最小
在算法执行中,\(J\)函数的值只会减少,不会增加
如何随机选择K个节点
- K必须小于m
- 随机选取K个样本做为K-均值算法的K个初始点
- K-均值算法可能收敛于局部最小值,所以需要多次运行算法,取J值最小的分类结果
如何选取K的值
- K值一般人工手动选取
- 有一些方法可以用于某些特定场景
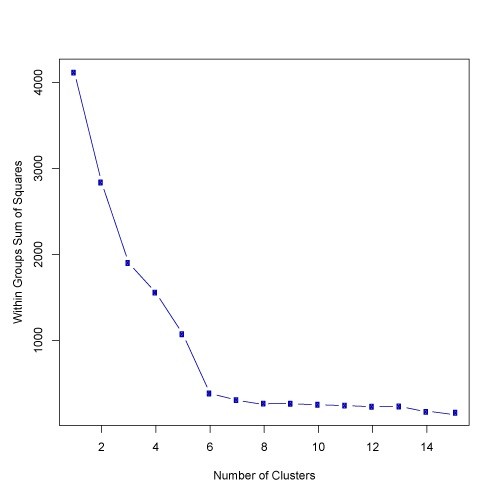
肘部法则(The elbow method):画出K值和函数J值的图像,如果随着K值的增加,J值先快速减少,并且后续平稳减少,则选取平稳减少开始的K的值
但更多的情况是,J值一直是平稳减少的,此时很难用此方法先出K的值
注意:随着K的增加,J的值总是减少的,如果J的值没有减少,则很可能收敛在了局部最小值
Lecture2: Dimensionality Reduction
维数约减(Dimensionality Reduction)
数据压缩
将一组相关性高的特征(如只是单位不同的数据),合并成一个特征
维度约减可以减少存储数据,并提高算法运行效率
数据可视化
超过3维的数据就不容易画出图来。所以多维的数据可以约减到2~3维,使得我们可以画出图来
主成分分析法(Principal Component Analysis)
主成分分析法(PCA)是最流行的维数约减算法
- 问题公式化
一个有两个特征的样本集合,在二维平面上,如果这些点大致集中在一条直线附近,那么我们可以将此二维的数据投影到这条直线上,得到目标的一维特征,这就实现了从二维到一维的维数约减
如果原样本有三个特征,且这些特征点大致分部在一个平面附近,那么可以选定这个平面,特征点投影到此平面的点为新的特征点,实现三维到二维的转换
PCA的目标是使得原样本到选定平面(或直线)之间的平均距离最小,这个平均距离称为投影误差(projection error)
从n维减到k维,需要找到k个n维的向量\(\mu^{(1)},\mu^{(2)},\cdots,\mu^{(k)}\),其中每一个\(\mu^{(i)} \in \mathbb{R}^n\)
- PCA与线性回归
线性回归求的是预测值与样本y值之间的距离平方,而PCA是样本点到投影点的距离
PCA算法步骤
- 先将特征均值规一化处理
- 计算协方差矩阵(covariance matrix)
算出来的\(\Sigma\)为\(n\times n\)的矩阵
公式用矩阵表示为
Sigma = (1/m) * X' * X;
- 计算\(\Sigma\)的特征向量(eigenvector)
[U,S,V] = svd(Sigma);
svd是奇异值分解函数(singular value decomposition)
这块用到的数据知识和证明todo
返回来的U值为\(n\times n\)矩阵,每一列为\(u^{(1)},u^{(2)},\cdots,u^{(n)}\)即为我们之前所要求的\(\mu^{(i)}\)
- 取U前k列计算新的特征值
约定\(z^{(i)}\)为\(x^{(i)}\)对应的新特征,则
\(z^{(i)} = U_{reduce}^T \cdot x^{(i)}\)
其中\(U_{reduce}\)为\(n \times k\)维矩阵,即U的前k列
- 完整的程序
Sigma = (1/m) * X' * X; % compute the covariance matrix
[U,S,V] = svd(Sigma); % compute our projected directions
Ureduce = U(:,1:k); % take the first k directions
Z = X * Ureduce; % compute the projected data points
从压缩后的数据恢复原始数据
\[\class{myMJSmall}{ x_{approx}^{(i)} = U_{reduce} \cdot z^{(i)} }\]可以从压缩后的数据近似地恢复原始数据
如何选择新维度k
\[\class{myMJSmall}{ \dfrac{\dfrac{1}{m}\sum^m_{i=1}||x^{(i)} - x_{approx}^{(i)}||^2}{\dfrac{1}{m}\sum^m_{i=1}||x^{(i)}||^2} \leq 0.01 }\]以上公式表明,99%的原始样本特征被保留了下来
- 算法步骤
令\(k=1,2,\dots\)
计算\(U_{reduce},z,x\)
检验算出来的结果是否大于99%,如果不是,则继续加大k的值。
- 使用svd返回值加速运算
\[\class{myMJSmall}{ \dfrac{\sum_{i=1}^kS_{ii}}{\sum_{i=1}^nS_{ii}} \geq 0.99 }\]使用svd返回的第二个值S来快速计算如何选择k
使用PCA的建议
PCA经常用来加速监督学习
PCA减少了数据存储所需要的磁盘空间,减少了算法运行时间
当选择k=2或者k=3时,可以将特征的图像展示出来
不应该使用PCA来过解决拟合问题,应该使用正规化
别假设你的算法需要PCA,先使用完整的样本进行训练,只有当你发现你需要PCA时,才使用PCA