Back to Posts

Jun 11, 2017

机器学习(Week7)-支持向量机/SVM(Support Vector Machines)

Posted in Tech

Lecture1: Support Vector Machines

优化目标（Optimization Objective）

逻辑回归

\[\class{myMJSmall}{ h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}} }\]

如果\(y = 1\)，则\(h_\theta(x) \approx 1\), \(\theta^Tx \gg 0\)
如果\(y = 0\)，则\(h_\theta(x) \approx 0\), \(\theta^Tx \ll 0\)

对于单个样本的代价函数

\[\class{myMJSmall}{ \begin{align} J(\theta) & = -ylog(h_\theta(x)) - (1-y)log(1- h_\theta(x)) \\ & = -ylog(\frac{1}{1+e^{-\theta^Tx}}) - (1-y)log(1 - \frac{1}{1+e^{-\theta^Tx}}) \end{align} }\]

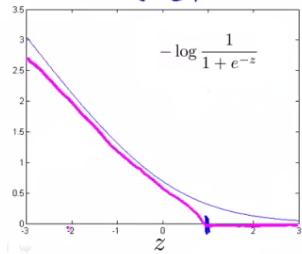
如果\(y = 1\)，令\(cost_1(z) = J(\theta) = -log(\frac{1}{1+e^{-z}})\); 其中\(z = \theta^Tx\)
\(cost_1\)的图案如下蓝线，如果我们用两条直线来近似此函数，则得到如下紫色线条（称之为hinge loss function）

cost_1

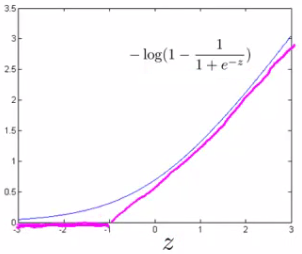
同理，如果\(y = 0\)，令\(cost_0(z) = J(\theta) = -log(1-\frac{1}{1+e^{-z}})\); 其中\(z = \theta^Tx\)
\(cost_0\)的图案如下蓝线，如果我们用两条直线来近似此函数，则得到如下紫色线条

cost_0

完整的代价函数

\[\class{myMJSmall}{ J(\theta) = \frac{1}{m}\sum_{i=1}^{m} \left [ -y^{(i)}log(h_\theta(x^{(i)})) - (1-y^{(i)})log(1- h_\theta(x^{(i)})) \right] + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2 }\]

使用cost函数代替

\[\class{myMJSmall}{ J(\theta) = \frac{1}{m}\sum_{i=1}^{m} \left [ y^{(i)}cost_1(\theta^Tx^{(i)})+ (1-y^{(i)})cost_0(\theta^Tx^{(i)}) \right] + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2 }\]

去掉\(m\)，并除以\(\lambda\)

\[\class{myMJSmall}{ J(\theta) = C\sum_{i=1}^{m} \left [ y^{(i)}cost_1(\theta^Tx^{(i)})+ (1-y^{(i)})cost_0(\theta^Tx^{(i)}) \right] + \frac{1}{2}\sum_{j=1}^{n}\theta_j^2 }\]

以上的\(C\)相当于\(\frac{1}{\lambda}\)，所以当过拟合时，可以通过减少\(C\)来实现；当欠拟合时，增加\(C\)的值

SVM的假设函数

\[\class{myMJSmall}{ h_\theta(x) = \begin{cases} 1 & \theta^Tx \ge 0 \\ 0 & otherwise \end{cases} }\]

大间距分类（Large Margin Classifiers）

对于之前给的代价函数

当\(y=1\)时，\(\theta^Tx \ge 1\) 才能使得代价函数为0
当\(y=0\)时，\(\theta^Tx \le -1\) 才能使得代价函数为0

在线性可分(Linearly Separale case)的分类问题上:

当\(C\)很大时，SVM算法决定的决策边界总是尽可能远离两个分类
决策边界与最近的点的距离称为间距(margin)
由于SVM的决策边界总是有很大的间距，所以SVM也叫大间距分类算法
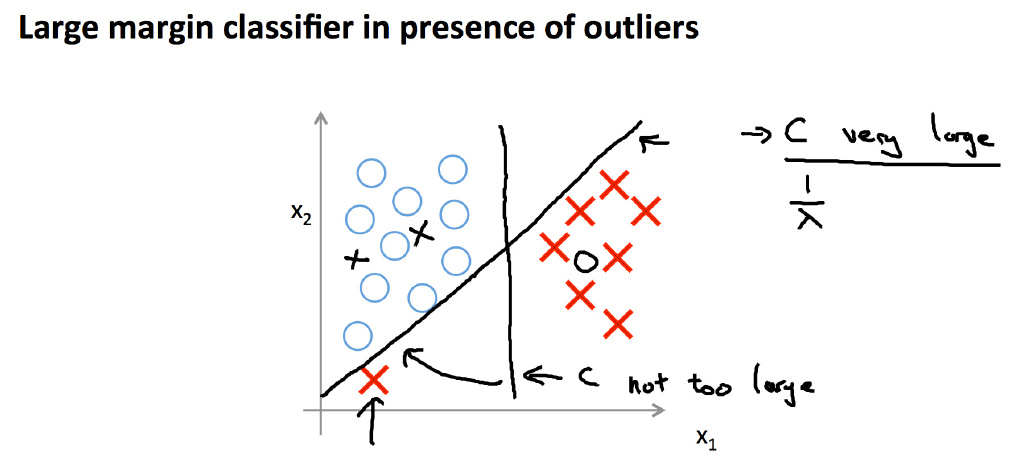
如果有一些异点（outlier），为了不影响大间距的特性，我们可以减小\(C\)的值

svm

大间距分类背后的数学原理

向量内积

\[\class{myMJSmall}{ u = \begin{bmatrix} u_1\\ u_2 \end{bmatrix} v = \begin{bmatrix} v_1\\ v_2 \end{bmatrix} }\]

符号\(\|u\|\)表示向量\(u\)的范数(norm)，也是向量\(u\)的长度，即(0,0)到\((u_1, u_2)\)的距离
\(\|u\| = \sqrt{u_1^2+u_2^2}\)
令\(p\)为向量\(v\)在\(u\)上的投影长度（当两向量夹角大于90度时，\(p\)为负数）
\(u^Tv = p\cdot\|u\|\)（证明todo）
\(u^Tv = v^Tu = u_1 v_1 + u_2 v_2\)

原\(\theta^Tx^{(i)} = p^{(i)}\cdot\|\theta\| = \theta_1 x_1^{(i)} + \theta_2 x_2^{(i)} + \cdots + \theta_n x_n^{(i)}\)
如果\(y = 1\)，要让代价为0，则需要\(\theta^Tx^{(i)} \ge 1\)，即\(p^{(i)} \ge 1\)
如果\(y = 0\)，要让代价为0，则需要\(\theta^Tx^{(i)} \le -1\)，即\(p^{(i)} \le -1\)
式子中的\(\theta\)为垂直于决策边界的向量（证明todo），如果使得上面的式子成立，则需要\(p\)的值尽可能的大，即决策边界到样本点之间的间距大

核函数(Kernels)

选定几个标记点\(l^{(1)},l^{(2)},\cdots l^{(i)}, \cdots\)
计算样本与标记点的相似度

\[\class{myMJSmall}{ \begin{align} f_i & = similarity(x, l^{(i)}) = exp(-\frac{\|x-l^{(i)}\|^2}{2\sigma^2}) \\ & = exp(-\frac{\sum_{j=1}^{n}(x_j-l_j^{(i)})^2}{2\sigma^2}) \end{align} }\]

此处的相似函数称为高斯核函数(Gaussian Kernel)，为核函数的一种
如果\(x \approx l^{(i)}\)，则\(f_i = \exp(-\dfrac{\approx 0^2}{2\sigma^2}) \approx 1\)
如果\(x\)距离\(l^{(i)}\)特别远，则\(f_i = \exp(-\dfrac{(large\ number)^2}{2\sigma^2}) \approx 0\)
此处的\(\sigma\)为高斯核函数的参数，影响特征分布的平滑程度

所有的标记点，通过核函数，就会得出一组新的特征和一个假设函数

\[\class{myMJSmall}{ \begin{align*} l^{(1)} \rightarrow f_1 \\ l^{(2)} \rightarrow f_2 \\ l^{(3)} \rightarrow f_3 \\ \dots \\ h_\theta(x) = \theta_1f_1 + \theta_2f_2 + \theta_3f_3 + \dots \end{align*} }\]

当\(h_\theta(x) \ge 0\)时，预测为1,其它情况预测为0

如何选取标记点

一种有效的选取标记点的方法是，选定每一个样本所在的点为标记点，则我们就有\(m\)个标记点
所以每一个样本，通过相似函数，可以得出\(m\)个特征值（或者\(m+1\)个，\(f_0 = 1\)）

\[\class{myMJSmall}{ x^{(i)} \rightarrow \begin{bmatrix} f_1^{(i)} = similarity(x^{(i)}, l^{(1)}) \\ f_2^{(i)} = similarity(x^{(i)}, l^{(2)}) \\ \vdots \\ f_m^{(i)} = similarity(x^{(i)}, l^{(m)}) \\ \end{bmatrix} }\]

求解

\[\class{myMJSmall}{ \min_{\theta} C \sum_{i=1}^m y^{(i)}\text{cost}_1(\theta^Tf^{(i)}) + (1 - y^{(i)})\text{cost}_0(\theta^Tf^{(i)}) + \dfrac{1}{2}\sum_{j=1}^n \theta^2_j }\]

以上也可以使用逻辑回归来求解，但由于SVM对计算过程中做了针对性的优化，使得使用SVM求解比逻辑回归等其它算法会快速很多。也由于如此，用于SVM的核函数几乎只能适用于SVM的算法。

参数选择

当C特别大时，将出现高方差，低偏差，更容易出现过拟合的问题
当C特别小时，将出现高偏差，低方差，更容易出现欠拟合的问题

对于\(\sigma^2\)，当\(\sigma^2\)偏大时，特征值\(f_i\)的分布更平滑，将出现高方差，低偏差，更容易出现过拟合的问题
当\(\sigma^2\)偏小时，特征值\(f_i\)的分布欠平滑，将出现低方差，高偏差，更容易出现欠拟合的问题

使用SVM

有许多现成的库

liblinear
libsvm

需要做的事情

选择参数C的值
选择合适的核函数：如果特征特别多，并且样本较少时，更适合不使用核函数（或者使用线性核函数/”linear” kernel）；当样本数量较多，并且特征较少时，更适合使用高斯核函数（需要确认\(\sigma^2\)的值）

注意事项

在使用高斯核函数时，需要先对特征值做归一化(feature scaling)
并非所有的相似函数都可以用做核函数，只有满足默塞尔定理(Mercer’s Theorem)，才能保证SVM中的数值计算等优化正确的在核函数上执行

验证

选取不一样的C值（如果是高斯核函数，也需要选取不一样的\(\sigma\)值），训练出对应的参数\(\theta\)，并使用交叉验证集合来选出最优的参数值。

多分类分类问题

许多SVM库内置多分类功能
可以使用与逻辑回归相似的one-vs-all方法，算出\(K\)组参数。预测时，假设函数值最大的那个分类即是预测分类

逻辑回归与SVM比较

当特征数量n相对于样本大小m很大时，使用逻辑回归，或者线性核函数的SVM
当n很小，并且m适中时，使用高斯核函数的SVM
当n很小，m很大时，应该手工添加一些多项式特征，并使用逻辑回归或者线性核函数的SVM
以上三种情况，神经网络都能处理得很好，但是可能会比较慢

学习资料

课件和笔记 Octave编程作业