Lecture1: Bias vs. Variance
下一步需要做什么
- 假设使用线性回归来预测房价,当训练好的预测函数无法应用于新房子的房价预测(预测值与实际偏差很大)时,我们应该如何改进?
获取更多的样本数据
减少特征项,保留更重要的特征项
添加特征项
加入多项式(\(x_1^2,x_2^2,x_1x_2\)等等)
增大\(\lambda\)值
减小\(\lambda\)值
- 但如何选择以上这些方法呢?
机器学习诊断: 诊断程序会评价学习算法是否有效,并给你下一步应该如何改进提供指引; 虽然实现会花点时间,但对提高算法很有帮助
评估假设函数
- 实际工作中由于太多特征无法画出曲线,所以需要有一种方法识别过拟合(high variance)
将样本数据分成两组: 一组训练集(70%); 一组是测试集(30%),表示为\((x_{test}^{(i)}, y_{test}^{(i)})\)
使用训练集学习得到参数\(\theta\)和预测函数
线性回归时,使用测试集计算代价函数:\(J_{test}(\theta) = \frac{1}{2m_{test}}\sum_{i=1}^{m_{test}}(h_\theta(x_{test}^{(i)}) - y_{test}^{(i)})^2\)
分类回归问题时,使用测试集计算代价函数:\(J_{test}(\theta) = -\frac{1}{m_{test}}\sum_{i=1}^{m_{test}}\left[ y_{test}^{(i)}log(h_\theta(x_{test}^{(i)})) + (1-y_{test}^{(i)})log(1-h_\theta(x_{test}^{(i)}) \right]\)
还可以使用误分率(Misclassification error or 0/1 Misclassification error)来计算测试集:
\(err(h_\theta(x),y) = \begin{cases} 1 & h_\theta(x) \ge 0.5 \, and\, y=0 \, or\, h_\theta(x) \lt 0.5 \,and\, y=1 \\ 0 & otherwise \end{cases}\\ \text{Test Error} = \dfrac{1}{m_{test}} \sum^{m_{test}}_{i=1} err(h_\theta(x^{(i)}_{test}), y^{(i)}_{test})\)
模型选择
- 例如我们以下线性回归模式,如何选择多项式的最高幂次?
\(h_\theta(x) = \theta_0 + \theta_1 x\)
\(h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2\)
\(h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3\)
\(\vdots\)
\(h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \cdots + \theta_{10}x^{10}\)
假设我们按之前的模型求出来\(\theta^{(1)},\theta^{(2)},\cdots,\theta^{(10)}\),并使用这些值计算出测试集合的误差\(J_{test}(\theta^{(1)}),J_{test}(\theta^{(2)}),\cdots,J_{test}(\theta^{(10)})\),则我们可以选择一个\(J\)最小的做为我们目标模型。
- 问题:如果我们使用测试集选出最合适的模型,那再使用测试集评估,是否有失公平?
解决此问题:将样本数据分成三组:训练集(60%),交叉验证集(Cross validation set)(20%),测试集(20%)
使用训练集学习以上各个模型的\(\theta\)值
使用交验验证集找取错误最小的模型
使用测试集评估模型泛化能力
诊断和解决欠拟合和过拟合的问题(Bias vs. Variance)
- 随着多项式的度数增加(degree of the polynomial),\(J_{train}\)和\(J_{cv}\)的变化如图
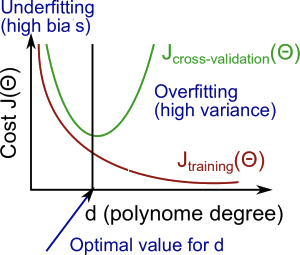
正规化与拟合问题
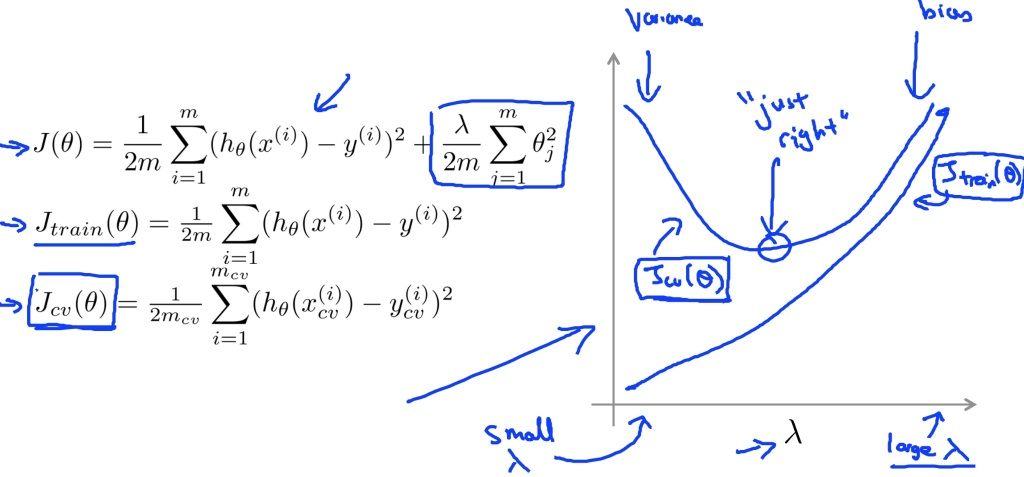
- 选择\(\lambda\)值
创建一系列的\(\lambda\)值:\(\lambda \in \{ 0, 0.01,0.02,0.04,0.08,0.16,0.64,1.28,2.56,5.12,10.24\}\)
像之前一样选取多种不同多项式的模型
每一个\(\lambda\)代入每一个模型,求出\(\theta\)值
使用这些计算出来的\(\theta\)值(假设函数),算出交叉验证集合的\(J_{cv}(\theta)\),注意,计算\(J\)时,\(\lambda=0\)
选出最优的模型和最优的\(\lambda\)
使用测试集合,来评估选出来的模型和\(\lambda\)值的泛化能力
学习曲线(Learning Curves)
- 欠拟合情况下,样本数量与训练集错误,测试集错误的关系
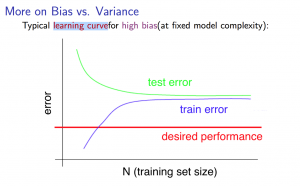
如果算法模型处理欠拟合状态,那么增加样本并不会有太大的改善
- 过拟合情况下,样本数量与训练集错误,测试集错误的关系
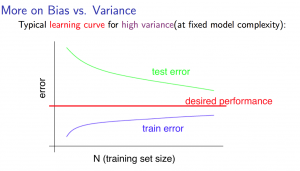
如果算法模型处于过拟合状态,那么可以通过增加样本来改善
回顾
获取更多的样本数据: 解决过拟合问题
减少特征项,保留更重要的特征项: 解决过拟合问题
添加特征项: 解决欠拟合问题
加入多项式(\(x_1^2,x_2^2,x_1x_2\)等等): 解决欠拟合问题
增大\(\lambda\)值: 解决过拟合问题
减小\(\lambda\)值: 解决欠拟合问题
神经网络中的拟合问题
参数过少的神经网络更容易引起欠拟合问题,不过他的计算量较小
大型神经网络(多个隐藏层,多个参数)更容易引起过拟合问题,需要使用正规化(\(\lambda\))来解决
Lecture2: Machine learning system design
创建垃圾邮件分类器
设计方案:选取10000~50000个单词,每一个单词是否存在做为一个输入特征,那么我们就会有10000~50000个特征,通过训练集中的这些特征训练出对应的预测函数(或者神经网络);给定对应的输入特征向量,即可预测此邮件是否为垃圾邮件
- 如何改善这个分类器
收集更多的数据(例如honeypot项目),但更多数据并不一定会有所改善
寻找更相关的特征,例如邮件的头信息等
输入使用更复杂的算法进行处理,比如不区分大小写,单复数等
以上不能靠直觉猜出哪个方法更有效,只能通过不断尝试来获取最做优解
错误分析
先用简单的算法快速实现,并在交叉验证集上测试
画出对应的学习曲线,分析并寻找有效的改善方法
错误分析:人工核实那些错误预测的验证集样例,找出共性,针对性地增加特征,或者对输入数据进行处理
偏斜类(Skewed classes)
当某一分类在样本集中占比特别小时,称之为偏斜类
偏斜类的存在导致无法判断错误率减少是否真正的改善了算法
衡量偏斜类的错误率
\[\class{myMJSmall}{ \begin{array}{c|c|c} & \text{Actual class 1} & \text{Actual class 0} \\ \hline \text{Predicted 1} & \text{true positive} & \text{false positive} \\ \hline \text{Predicted 0} & \text{false negative} & \text{true negative} \end{array} }\]- 查准率(Precision)
- 召回率(Recall)
- 权衡
以上两个指标可以很好的衡量算法是否工作。我们期望这两个指标越高越好
如果提高预测为1的阈值,例如\(h_\theta(x) \ge 0.7\)时,才预测为1,其它结果预测为0,则这将导致查准率上升,召回率下降;反之,如果将阈值调小成0.3,则查准率下降,召回率上升。
可以使用F值(F score/F1 score)来衡量阈值是否合适: \(\text{F Score} = 2\dfrac{PR}{P + R}\)
数据
- 我们需要多少数据来训练?
一般而言,一个较差的算法,使用大量的样本进行训练,会比一个优秀算法,只用少量数据训练来得更有效
我们选择的特征应该包含足够多的信息,例如给定一个输入,对应领域的专家可以准确预测结果
如果我们选择一个低偏差(low-bias)模型(一般含有大量的特征,多层隐藏层等),那么越多的数据,我们得到的预测函数将会越精准