Back to Posts

机器学习(Week5)-反向传播(BP)

Posted in Tech

Lecture1: Backpropagation

神经网络的代价函数

\[\class{myMJSmall}{ J(\Theta) = -\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^K \left[ y_k^{(i)}log((h_\Theta(x^{(i)}))_k) + (1-y_k^{(i)})log(1- (h_\Theta(x^{(i)}))_k) \right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_{l+1}}(\Theta_{j,i}^{(l)})^2 }\]

\(L\): 表示神经网络的层数
\(s_l\): 表示第\(l\)层的激活单元数量（不算上偏置单元bias unit）
\(K\): 表示输出层单元数量（分类数量）；\(s_L=K\)
\(h\Theta(x) \in \mathbb{R}^{K}, (h\Theta(x))_j\)表示第\(j\)个输出
\(y \in \mathbb{R}^{K}\)，例如有4种分类，那么如果\(y\)属于第1个分类，则记做 \(\class{myMJSmall}{ \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix} }\)

以上代价函数，第一部分两次求和：每一个输出单元，使用逻辑回归的代价算法计算后相加
第二部分三次求和：将所有\(\Theta\)中每一个元素（除偏置单元外）的平方相加

反向传播算法（Backpropagation algorithm）

  • 目标

我们已经知道如何计算\(J(\Theta)\)，如果要求出使得\(J(\Theta)\)最小时\(\Theta\)的值
需求计算\(\frac{\partial}{\partial\Theta_{ij}^{(l)}} J(\Theta)\)

  • 正向传播（Forward propagation）
\[\class{myMJSmall}{ \begin{align} & a^{(1)} = x \\ & z^{(2)} = \Theta^{(1)}a^{(1)} \\ & a^{(2)} = g(z^{(2)}) & (add \, a_0^{(2)}) \\ & z^{(3)} = \Theta^{(2)}a^{(2)} \\ & a^{(3)} = g(z^{(3)}) & (add\, a_0^{(3)}) \\ & \vdots \\ & z^{(L)} = \Theta^{(L-1)}a^{(L-1)} \\ & a^{(L)} = h_\Theta(x) = g(z^{(L)}) \\ \end{align} }\]
  • 反向传播（Backpropagation）
\[\class{myMJSmall}{ \begin{align} & \delta_j^{(L)} = a_j^{(L)} - y_j & (\delta^{(L)} = a^{(L)} - y) \\ & \delta^{(L-1)} = (\Theta^{L-1})^T\delta^{(L)} .* g'(z^{(L-1)})\\ & \delta^{(L-2)} = (\Theta^{L-2})^T\delta^{(L-1)} .* g'(z^{(L-2)})\\ & \vdots \\ & \delta^2 = (\Theta^{2})^T\delta^{(3)} .* g'(z^{(2)}) \end{align} }\]

直觉上，我们把\(\delta_j^{(l)}\)看做第\(l\)层，第\(j\)个单元的误差，而事实上这是一个函数偏导（todo 待细说明）
我们先算出输出层的\(\delta\)，然后一层一层反向推出前面的误差，所以此算法叫反向传播算法，由于\(\delta\)是误差，所以也叫做误差反向传播算法
没有\(\delta^{(1)}\)，因为第一层是输入层，是观察的变量，不存在误差
上述式子中\(g'(z^{(l)}) = a^{(3)}.*(1-a^{(3)})\)，推导过程todo
\(\frac{\partial}{\partial\Theta_{ij}^{(l)}} J(\Theta) = a_j^{(l)}\delta_i^{(l+1)} (\lambda = 0)\)，推导过程todo
不存在\(\delta^{(l)}_0\)

  • 算法描述

给定一个样本集合\(\{(x^{(1)},y^{(1)}) \cdots (x^{(m)},y^{(m)}) \}\)
初使化：
设置\(\Delta^{(l)}_{ij} = 0\)。即创建若干个与\(\Theta^{(1)}, \Theta^{(2)} \cdots \Theta^{(L-1)}\) 维度相同的矩阵，每一个元素都为0
循环遍历整个样本，\(for \, t=1:m\)
(1) 设置\(a^{(1)} = x^{(t)}\)
(2) 使用正向传播算出\(a^{(l)}, a^{(l)} ; l \in \{2,3,\cdots L\}\)
(3) 使用\(y^{(t)}\)计算\(\delta^{(L)} = a^{(L)} - y^{(t)}\)
(4) 使用反向传播计算\(\delta^{L-1}, \delta^{L-2},\cdots \delta^{2)}\)
(5) 更新\(\Delta: \Delta^{(l)}_{ij} := \Delta^{(l)}_{ij}+a_j^{(l)}\delta_i^{(l+1)};\) 或者使用矩阵形式：\(\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T\)
循环结束

\[\class{myMJSmall}{ \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta) = D_{ij}^{(l)} = \begin{cases} \frac{1}{m}\left(\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)} \right ) & j \neq 0; \\ \frac{1}{m}\Delta_{ij}^{(l)} & j = 0; \end{cases} }\]

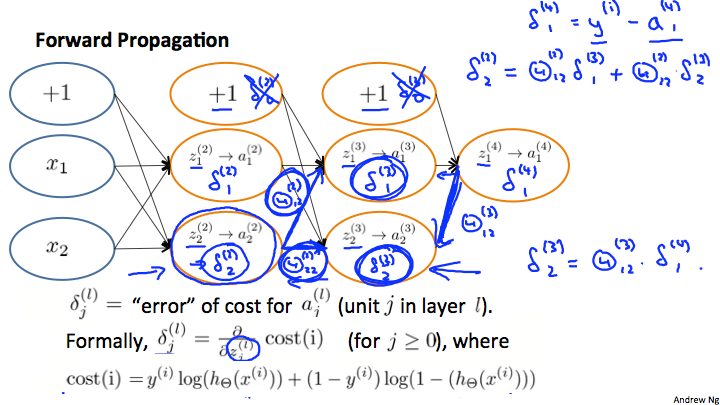
\(\delta\)的含义

令\(cost(t) =y^{(t)} \ \log (h_\Theta (x^{(t)})) + (1 - y^{(t)})\ \log (1 - h_\Theta(x^{(t)}))\)
\(\delta_j^{(l)} = \frac{\partial}{\partial z_j^{(l)}}cost(t)\)
即\(\delta\)表示\(cost(t)\)的斜率，斜率越大，则表示偏离越多，结果越不正确，所以\(\delta\)直观上看错误差

delta计算

实战技巧

  • 参数展开

由于神经网络中的参数\(\Theta\)都为数组，而像fminunc这样的Octave函数接收的theta都为向量，所以需要将\(\Theta\)展开成向量传入函数，在计算时再转换成数组
令\(\Theta^{(1)},\Theta^{(2)},\Theta^{(3)}\)在Octave中的表示变量为Theta1, Theta2, Theta3
令\(D^{(1)},D^{(2)},D^{(3)}\)在Octave中的表示变量为D1, D2, D3
则展开表示为

thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]

假设 Theta1 的维度为 10x11, Theta2 为 10x11 , Theta3 为 1x11
则还原使用reshape函数，表示为

Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)
  • 正确性检查

由导数的定义： \(\dfrac{\partial}{\partial\Theta}J(\Theta) \approx \dfrac{J(\Theta + \epsilon) - J(\Theta - \epsilon)}{2\epsilon}\)
所以我们可以使用以下代码算出偏导的近似值:

epsilon = 1e-4;
for i = 1:n,
	thetaPlus = theta;
	thetaPlus(i) += epsilon;
	thetaMinus = theta;
	thetaMinus(i) -= epsilon;
	gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;

使用此代码算出的结果与我们之前算的偏导数比较，如果相差不多，则表示之前的算法实现是正确的
注意: 当检查完算法实现正确之后，一定要关闭正确性检查，不然会使用算法特别慢

  • 随机化初使\(\Theta\)

在神经网络算法中，如果将初使权值都设置成0，则在每一次更新后，得到的新权值也会一样，此现象称之为对称现象(symmetric)
使用随机的初使值：初使化每一个\(\Theta^{(l)}_{ij}\)的值在区间\([-\epsilon,\epsilon]\)内，实现如下：

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

此处的Theta1,2,3 维度与之前相同
rand(a,b)创建一个axb维的数组，值介与0到1之间

综合说明

  • 架构的选取

输入单元为特征数
输出单元为分类数
隐藏层的单元数：越多越好，平衡增加单元数带来的收益和开销
一般地：一个隐藏层，如果有多个隐藏层，建议每一个隐藏层的单元数一致

  • 训练神经网络

随机初使化参数
实现正向传播计算出\(a, z,h\)
计算代价函数\(J\)
通过反向传播计算出偏导
使用近似计算的偏导检查算法实现的正确性，然后关闭检查
使用梯度下降或者其它优化算法算出Theta值

  • 图示

梯度下降

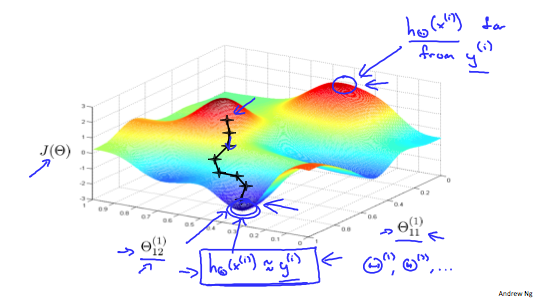
\(J(\Theta)\)已经不是凸函数了，所以通过梯度下降查找到的值可能是局部最小值（local minimum）

学习资料

课件和笔记 Octave编程作业

Read Next

机器学习(Week4)-神经网络