May 24, 2017

机器学习(Week4)-神经网络

Posted in Tech

Lecture1: Neural Networks

为什么我们需要神经网络

当特征特别多（计算机视觉问题）时，如果计算多次多项式，得出来的最终特征会特别多，多到计算机无法处理。

产生的原因

Algorithms that try to mimic the brain. Was very widely used in 80s and early 90s; popularity diminished in late 90s
Recent resurgence: State-of-the-art technique for many applications

One learning algorithm

大脑的某一块区域（听觉皮层）能处理听觉，视觉，触觉等相关的信息（神经重接实验），所以是否有一各机器学习算法，可以处理各种的事务？

模型表示（Model Representation）

最简单的表示（只有一个神经元的情况下）

\[\class{myMJSmall}{ \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} \rightarrow \begin{bmatrix} \end{bmatrix} \rightarrow h_\theta(x) }\]

模拟神经元：输入特征\(x_1\cdots x_n\)像是神经元树突(dendrites)；输出结果\(h_\theta(x)\)好比神经轴突(axons)
\(x_0\)的值总是为1，称之为偏置单元（bias unit），有时候会不画出来，计算维度时也不计入
神经网络中也使用\(\frac{1}{1+e^{\theta^Tx}}\)，称之为S型激活函数（sigmoid/logistic activation function）
\(\theta\)参数有时候也称之为权重(weight)

添加层数

\[\class{myMJSmall}{ \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} \rightarrow \begin{bmatrix} a_1^{(2)} \\ a_2^{(2)} \\ a_3^{(2)} \\ \end{bmatrix} \rightarrow \begin{bmatrix} a_1^{(3)} \\ \end{bmatrix} \rightarrow h_\theta(x) }\]

\(x_0,x_1\cdots\)所在的层称为第一层（layer 1)，也称之为输入层（input layer）
\(h_\theta(x)\)的前一层（layer 3）输出称之类输出层（output layer)
在输入层与输出层之间的层（layer 2）称为隐藏层（hidden layer）
隐藏层中的\(a_0^{(2)},a_1^{(2)}\cdots\)称为激活单元（activation units）

激活单元的表示

\[\class{myMJSmall}{ \begin{align*} a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \\ a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \\ a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \\ h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) \\ \end{align*} }\]

\(a_i^{(j)}\)表示第\(j\)层的第\(i\)个激活单元
\(\Theta^{(j)}\)表示从第\(j\)层到\(j+1\)层的函数参数矩阵
\(\Theta^{(j)}\)的维度计算方法为：\(s_{j+1}\times (s_j+1)\)，其中\(s_j\)为第j层的激活单元个数（不包括为0的单元）
之前的\(\Theta^{(1)}\)的维度为\(3\times4\)，\(\Theta^{(2)}\)的维度为\(1\times 4\)
函数\(g\)为S型函数(sigmoid function)

向量表示

\[\class{myMJSmall}{ a_1{(2)} = g(z_1^{(2)}) \\ a_2{(2)} = g(z_2^{(2)}) \\ a_3{(2)} = g(z_3^{(2)}) \\ \\ a_1{(3)} = g(z_1^{(3)}) \\ }\]

其中

\[\class{myMJSmall}{ z_k^{(2)} = \Theta_{k,0}^{(1)}x_0+\Theta_{k,1}^{(1)}x_1 +\cdots + \Theta_{k,n}^{(1)}x_n \\ z_k^{(3)} = \Theta_{k,0}^{(1)}a_0+\Theta_{k,1}^{(1)}a_1 +\cdots + \Theta_{k,n}^{(1)}a_n \\ }\]

更一般的

\[\class{myMJSmall}{ z_k^{(j)} = \Theta_{k,0}^{(j-1)}x_0 + \Theta_{k,1}^{(j-1)}+\cdots+\Theta_{k,n}^{(j-1)}x_n \\ }\]

令

\[\class{myMJSmall}{ x = \begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_n\\ \end{bmatrix} a^{(j)} = \begin{bmatrix} a_0^{(j)} \\ a_1^{(j)} \\ \vdots \\ a_n^{(j)} \\ \end{bmatrix} z^{(j)} = \begin{bmatrix} z_0^{(j)} \\ z_1^{(j)} \\ \vdots \\ z_n^{(j)} \\ \end{bmatrix} }\]

且

\[\class{myMJSmall}{ a^{(1)} = x }\]

则，向量表示为

\[\class{myMJSmall}{ z^{(j)} = \Theta^{(j−1)}a^{(j−1)}\\ a^{(j)} = g(z^{(j)})\\ j \in [2,3\cdots] }\]

例子

AND运算

\[\class{myMJSmall}{ \begin{align*}\begin{bmatrix}x_0 \newline x_1 \newline x_2\end{bmatrix} \rightarrow\begin{bmatrix}g(z^{(2)})\end{bmatrix} \rightarrow h_\Theta(x)\end{align*} }\]

假设我们有两个特征值\(x_0, x_1\)，值只能取0和1

令\(\class{myMJSmall}{\Theta_{(1)} = \begin{bmatrix}-30 & 20 & 20 \end{bmatrix}}\)，则可以得到以下结果

\[\class{myMJSmall}{\begin{array}{cc|c} x_1 & x_2 & h_\theta(x) \\ \hline 0 & 0 & g(-30) \approx 0 \\ 0 & 1 & g(-10) \approx 0 \\ 1 & 0 & g(-10) \approx 0 \\ 1 & 1 & g(10) \approx 1 \\ \end{array} }\]

OR运算与NOR运算

同理，我们可以得到如下

\[\class{myMJSmall}{ NOR: \Theta^{(1)} = \begin{bmatrix} 10 & -20 & -20 \end{bmatrix} \\ OR: \Theta^{(1)} = \begin{bmatrix}-10 & 20 & 20\end{bmatrix} }\]

XNOR异或非运算

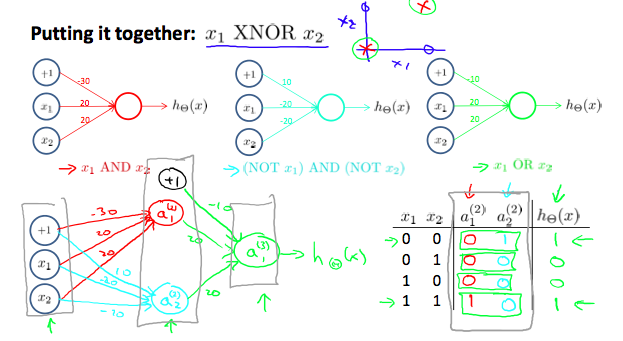
使用AND，NOR，OR和神经网络结合成XNOR运算

\[\class{myMJSmall}{ \begin{align*}\begin{bmatrix} x_0 \\ x_1 \\ x_2 \end{bmatrix} \rightarrow \begin{bmatrix} a_1^{(2)} \\ a_2^{(2)} \end{bmatrix} \rightarrow \begin{bmatrix} a^{(3)} \end{bmatrix} \rightarrow h_\Theta(x) \end{align*} }\] \[\class{myMJSmall}{ \Theta^{(1)} =\begin{bmatrix}-30 & 20 & 20 \newline 10 & -20 & -20\end{bmatrix} \\ \Theta^{(2)} =\begin{bmatrix}-10 & 20 & 20\end{bmatrix} }\]

过程如下图 xnor

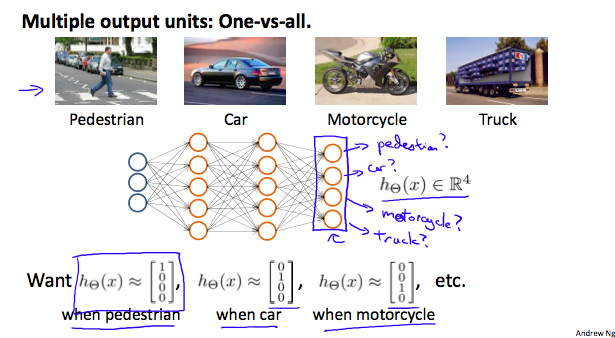
多分类分类问题（Multiclass Classification）

此时输出层包含有多个\(h_\theta(x)\)函数，即为向量。每一列代表属于所属分类的概率，取概率最大的为对应的预测值

如下图，\(n\)个特征，预测4个分类

\[\class{myMJSmall}{ \begin{align*}\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \rightarrow \begin{bmatrix} a_0^{(2)} \\ a_1^{(2)} \\ a_2^{(2)} \\ \vdots \end{bmatrix} \rightarrow \begin{bmatrix} a_0^{(3)} \\ a_1^{(3)} \\ a_2^{(3)} \\ \vdots \end{bmatrix} \rightarrow \cdots \rightarrow \begin{bmatrix} h_\theta(x)_1 \\ h_\theta(x)_2 \\ h_\theta(x)_3 \\ h_\theta(x)_4 \\ \end{bmatrix} \end{align*} }\]

如下图

学习资料

课件和笔记 Octave编程作业