Lecture1: Classification and Representation
分类问题(Classification)
二元分类问题(Binary Classification)
\[\class{myMJSmall}{y \in \{0,1\}}\]\(y\)只有两个值(即分成两类)
标记为0的分类:也叫负类(Negative Class),例如0代表良性肿瘤
标记为1的分类:也叫正类(Positive Class),例如1代表恶性肿瘤
预测函数/逻辑回归(Logistic Regression)
\[\class{myMJSmall}{h_\theta(x) = g(\theta^Tx) \\ g(z) = \frac{1}{1+e^{-z}} \\ 即 h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}}\]\(0 \le h_\theta(x) \le 1\)
\(g(z)\)称为S型函数(Sigmoid function)或逻辑函数(Logistic function)
\(h_\theta(x)\)值表示\(y=1\)的概率值,即\(h_\theta(x) = P(y=1\mid x;\theta) = 1-P(y=0\mid x;\theta)\)
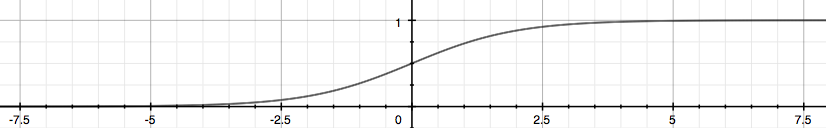
x=-10:0.01:10;
y=1./(1+e.^(-x));
plot(x,y);
决策边界(Decision Boundary)
- \(h_\theta(x)\ge0.5\)我们预测\(y=1\); \(h_\theta(x)\lt0.5\)我们预测\(y=0\)
- 根据\(g(z)\)函数的特性,如果\(g(z)\ge0.5\),则\(z\ge 0\),即\(\theta^Tx\ge 0\)
- 决策边界即为\(y=1\)和\(y=0\)分割线
例如:\(\theta^Tx=-3+x_1+x_2\),令\(y=1\),则\(-3+x_1+x_2\ge0\),由此函数可以得到\(x1, x2\)平面内的一条直线为决策边界
若函数\(z\)为非线性,比如\(z=-1+x_1^2+x_2^2\),则决策边界为一个圆
代价函数
-
如果使用线性回归中的代价函数,则\(J(\theta)\)呈现为波浪型,即有许多的局部最小值;此函数称为非凸函数(Non-convex function)
-
所以使用以下代价函数
样本中\(y=1\),如果\(h_\theta(x)\)求得结果也为1,则结果与预测吻合,代价函数值为0;如果\(h_\theta(x)\)求得结果为0,表示结果与预测相违背,代价函数值为无穷大。
\(y=0\)同理
- 简化代价函数
- 梯度下降
形式与线性回归一致,证明 todo
高级优化
- 其它优化算法
Conjugate gradient(共轭梯度法)
BFGS(变尺度法)
L_BFGS(限制变尺度法)
- 特点
不用手动选择\(\alpha\)
一般来说比梯度下降法快
但是更加复杂
- 使用Octave提供的这些算法
fminunc @todo
多分类分类问题(Multiclass Classification/One Vs All)
\[\class{myMJSmall}{y \in \{0,1\cdots,n\}}\]- 将此分类问题转化成n+1个二元分类问题,即多个\(h_\theta(x)\)函数,每一个计算属于当前分类的概率,取概率最大的\(y\)值为预测值
Lecture2: Solving the Problem of Overfitting
过拟合问题(Overfitting)
- 如果特征太多,那么假设函数的曲线会通过每一样本(每一个样本按假设函数算出来的y值都与样本的y值一致),即\(J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2\approx 0\),但是不能泛化(generalize)到新样本。
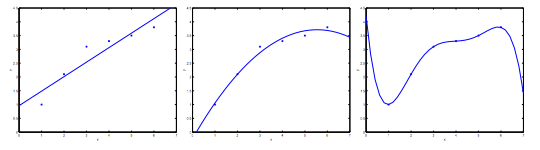
上图1,欠拟合(Underfitting),或者高偏差(High bias)
上图2,拟合效果很好(Just right)
上图3,过拟合(Overfitting),或者高方差(High variance)
解决过拟合问题
- 减少特征的数量
人工选择更重要的特征
模型选择算法,自动选择使用哪些特征(后续会学到)
缺点:舍弃特征相当于舍弃了一些信息
- 正规化(Regularization)
保留所有的特征,但减小\(\theta_j\)的量级
当有很多特征,并且每一个特征都对结果有点贡献时,正规化可以很好的工作
正规化
正规化线性回归
- 修改代价函数
\(\lambda\)称为正规化参数(regularization parameter),如果\(\lambda\)很小,则求出来的\(\theta\)会很好的拟合样本数据(过拟合),如果\(\lambda\)很大,则\(\theta\)会变得很小,求出来的结果会是较光滑的曲线。
- 梯度下降
当\(j\ge1\)时,式子可以写成\(\theta_j = \theta_j(1-\alpha\frac{\lambda}{m}) - \frac{\alpha}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\),可以看出来正规化后,每一次迭代\(\theta_j\)都会比无正规化前小一点。
- 正规方程
正规化之后由于添加了\(\lambda\cdot L\)使得原来可能不可逆的\(X^TX\)变得可逆了
正规化逻辑回归
- 代价函数
- 梯度下降的方程与线性梯度下降方程一致