有图有真相。
看到一个函数,不管你是想知道他的趋势如何,或者有人说他有一个漂亮的函数图像,我们都要画出这个函数的图来确认。
比如有人跟你说
f(x) = sin(4*x)
是一个玫瑰方程式,在看到图像之前绝对会一脸蒙逼。所以如果能有一个显示出函数图像的工具,会提升你的浪漫值和幸福感。
网页是一个快速开发的好东西,而canvas正好能实现这个需求。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~幸福的分割线~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
canvas 基础
创建一个canvas
首先,创建一个空的canvas,宽高为800x400
<html>
<head>
<meta charset="utf-8">
<title>画出你的函数</title>
</head>
<body>
<canvas id="myCanvas" width="800px" height="400px" style="border:1px solid lightgrey;">
你的浏览器不支持canvas
</canvas>
</body>
</html>
canvas的坐标原点(0,0)在画布的左上角,x轴延水平从左向右递增,y轴从上到下递增。y轴的方向与常规的坐标系方向相反。
使用javascript画图
ctx = document.getElementById("myCanvas").getContext("2d");
ctx.strokeStyle="lightgreen";
ctx.fillStyle="lightblue";
ctx.moveTo(20, 20);
ctx.lineTo(200, 300);
ctx.stroke();
ctx.fillRect(300, 20, 200, 300);
ctx.beginPath();
ctx.arc(700,180,90,0,2*Math.PI);
ctx.stroke();
使用getContext(“2d”)获取到2d的绘图环境(CanvasRenderingContext2D),目前并没有3d这个参数值,3d做图可以使用WebGL。
strokeStyle和fillStyle分别是笔触的样式和填充的样式,不仅可以是单一的颜色,也可以是一个渐变的对象(如createLinearGradient等)。
画直线使用moveTo来确认起始点,使用lineTo来确认结束点,stroke绘制路径。可以通过添加lineTo的调用来绘制折线。
画长方形使用fillRect,这个方法绘制的图形是填充的,如果只要描边,使用strokeRect方法。
画圆使用了一个画弧线的函数,参数依次是圆心坐标x, y,半径,起始角度,结束角度,是否是顺时针。例子中没有显示最后一个参数。
以下是arc函数角度值规定的图例。
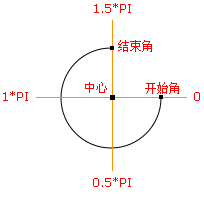
如何画一个点
并没有提供直接画点的函数,但可以用以下方法画出点来(参见此)
ctx = document.getElementById("myCanvas").getContext("2d");
ctx.strokeStyle="lightgreen";
ctx.fillStyle="lightgreen";
ctx.beginPath();
ctx.moveTo(2,1);
ctx.lineTo(3,2);
ctx.stroke();
ctx.fillRect(2,5,1,1);
ctx.beginPath();
ctx.arc(2, 10, 1, 0, 2 * Math.PI, true);
ctx.fill();
ctx.beginPath();
ctx.arc(2, 15, 0.5, 0, 2 * Math.PI, true);
ctx.fill();
画出来的效果和放大500%后的效果:


画出函数
坐标系转换
按正常,我们把canvas的中心点(200,400)点做为坐标的函数的原点,所以我们需要将函数的坐标点映射成canvas上的点(也可以使用transform函数来实现)
var canvas = document.getElementById("myCanvas");
var cw = canvas.width
var ch = canvas.height
var ctx = canvas.getContext("2d")
// (x, y)正常坐标系上的点,(cx, cy)为canvas里的坐标点
function drawLine(x1, y1, x2, y2){
var cx1 = x1+cw/2
var cx2 = x2+cw/2
var cy1 = ch/2-y1
var cy2 = ch/2-y2
ctx.moveTo(cx1, cy1)
ctx.lineTo(cx2, cy2)
ctx.stroke()
}
function drawPoint(x, y){
var cx = x+cw/2
var cy = ch/2-y
ctx.fillRect(cx, cy, 1, 1)
}
画出对应的函数
有了之前的这些准备,画了一函数的图就很容易,x取-cw/2到cw/2,求出对应的y值,画出对应的点即可展示出函数的图。
将之前的代码整理一下,创建一个FuncDraw的函数对象(Function Object),并添加clear等辅助的方法。
drawFx和drawFxNow分别定义有动画和无动画的绘制函数。
function FuncDraw(canvas) {
this.canvas = canvas
var cw = canvas.width
var ch = canvas.height
var ctx = canvas.getContext("2d")
var ticker = new Array();
// 每一次x的取值增加多少
var step = 0.01
// 每一毫秒画几个点
var pointsPerMillisecond = 100
this.setConfig = function(s, p){
step = s
pointsPerMillisecond = p
}
this.clear = function (){
var len = ticker.length
if(len != 0){
for(var i = 0; i < len; i++){
clearInterval(ticker[i])
}
ticker = new Array()
}
ctx.clearRect(0, 0, cw, ch);
}
this.setColor = function (stroke, fill){
ctx.strokeStyle = stroke
ctx.fillStyle = fill
}
// (x, y)正常坐标系上的点,(cx, cy)为canvas里的坐标点, ctx为canvas绘图环境
this.drawLine = function (x1, y1, x2, y2){
var cx1 = x1+cw/2
var cx2 = x2+cw/2
var cy1 = ch/2-y1
var cy2 = ch/2-y2
ctx.moveTo(cx1, cy1)
ctx.lineTo(cx2, cy2)
ctx.stroke()
}
this.drawPoint = function (x, y){
var cx = x+cw/2
var cy = ch/2-y
ctx.fillRect(cx, cy, 1, 1)
}
// 画出x轴和y轴
this.drawCoords = function (){
this.drawLine(-cw/2, 0, cw/2, 0);
this.drawLine(0, ch/2, 0, -ch/2);
}
// 画直角坐标系的函数图像,不带动画
this.drawFxNow = function (f, scalex, scaley){
for(var x=-cw/2; x<cw/2; x+=step){
this.drawPoint(x, f(x*scalex) * scaley)
}
}
// 画直角坐标系的函数图像,带动画
this.drawFx = function (f, scalex, scaley){
var dp = this.drawPoint
var currentx = -cw/2
var t = setInterval(function(){
for(var i=0; i<pointsPerMillisecond; i++){
dp(currentx, f(currentx*scalex) * scaley)
currentx += step
}
if(currentx > cw/2){
clearInterval(t)
}
}, 1)
ticker.push(t)
}
}
像 f(x)=x*x 这样的函数,y值增长过快,导致在最左点的y值超过了canvas的范围,所以drawFx和drawFxNow函数提供了scaley参数(scalex同理)。
为了演示多个例子,我们创建的多个canvas,分别是c1, c2, c3…。在每一个绘图区域上点击,将会重画对应的图案(仅限有动画)。
var canvas = document.getElementById("c1");
c1 = new FuncDraw(canvas);
c1.setColor("lightgrey", "red")
canvas.onclick = function(){
c1.clear()
c1.drawCoords()
c1.drawFx(function(x){ return x*x;}, 1, 0.005)
}
canvas.click()
猜猜下图都是些什么函数
画一个心(点击出动画)
心是由两个函数组成(以下公式展示由MathJax支持)
`y = -sqrt(1-x^2)+x^(2/3)`
转成javascript函数如下
function(x){
return Math.sqrt(1-x*x) + Math.pow(x * x, 1/3)
}
function(x){
return -Math.sqrt(1-x*x) + Math.pow(x * x, 1/3)
}
极坐标系下的函数图像
还记得文章开始说的这个函数吗:f(x) = sin(4*x)。输入后发现并没有出现啥浪漫的图案啊?只是一个正常的正弦曲线罢了!
原因是这个函数需要在极坐标系下才能展示出漂亮的图来,所以准确的函数表示应该是r = sin(4θ)。
坐标系转换思路
极坐标即确定一个极点和从极点出发的一条射线(极轴),通过与极轴的夹角和到极点的距离确定平面内的一个点。
我们假定直角坐标系的原点为极点,x轴的正方向部分为极轴,则平面内的点(θ, r)如图所示。
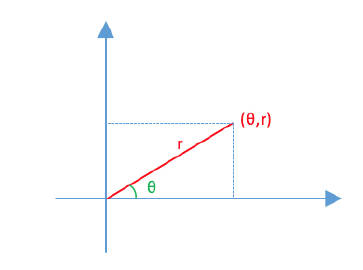
从图上也可以很清楚地看出两个坐标系的转换关系
x = r*cos(θ)
y = r*sin(θ)
画出函数图像
根据之前的坐标转换公式,很容易写出一个按极坐标画函数的方法
// 画极坐标系的函数,不带动画
this.drawPolarFxNow = function(fpolar, scalex, scaley){
for(var sita=0; sita < 6*Math.PI; sita+=0.01){
var r = fpolar(sita)
var x = r*Math.cos(sita)
var y = r*Math.sin(sita)
this.drawPoint(x*scalex, y*scaley);
}
}
// 画极坐标系的函数,带动画
this.drawPolarFx = function(fpolar, scalex, scaley){
var dp = this.drawPoint
var currentSita = 0
var t = setInterval(function(){
for(var i=0; i<pointsPerMillisecond; i++){
var r = fpolar(currentSita)
var x = r*Math.cos(currentSita)
var y = r*Math.sin(currentSita)
dp(x*scalex, y*scaley)
currentSita += step
}
if(currentSita > 100*Math.PI){
clearInterval(t)
}
}, 1)
ticker.push(t)
}
其中的θ取值范围为0到100π,相当于绕点50圈。这个值设置大点是为了再画动画时,能让整个周期持续时间更长,也让线看上去更完整,拟补step太大带来的点分布稀疏问题。
例子
接下为是几个函数的例子(点击可重绘)
玫瑰花瓣曲线,以下图案是由5个方程式组成。
r = 5sin(4θ)
r = 4sin(4θ)
r = 3sin(4θ)
r = 2sin(4θ)
r = 1sin(4θ)
r = 5cos(πθ)
r = 5cos(2θ)
r = 5cos(3θ)
r = 5cos(4θ)
r = 5cos(5θ)
r = 5cos(6θ)
r = 5cos(7θ)
r = 0.1θ
r = 1+|4sin(4θ)|
r = 2+|4sin(4θ)|
r = 3+|4sin(4θ)|
r = 4+|4sin(4θ)|
你的函数(极坐标)
输入你的函数(js function):
送一个x,y随时间变化的函数曲线
x = sin(m*t)
y = sin(n*t)
以下曲线为m = 13, n = 18 (参考此)